Question

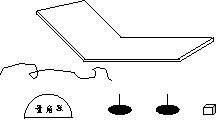
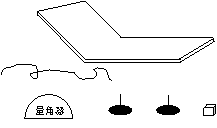
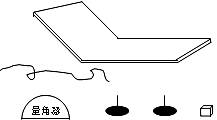
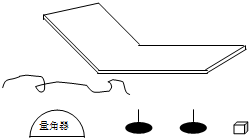如图示的器材是：木质轨道（其倾斜部分倾角较 大，水平部分足够长）、小铁块、一根细线、一个量角器．只用上述器材就可以测定小铁块和木质轨道间的动摩擦因数，实验步骤是：
a．将小铁块从倾斜轨道上的一固定位置由静止释放，让小铁块能下滑到水平轨道上
b．用图钉把细线钉在小铁块运动的起点、终点处并拉直
c．用量角器测量

细线与水平轨道平面的夹角θ

（先用文字说明再用字母表示），则小铁块与木质轨道间的动摩擦因数可表示为μ=

tanθ

．

Answer 1

分析：物块在下滑到停止的过程中，有重力做功和摩擦力做功，根据动能定理求出动摩擦因数的表达式，从而确定要测量的物理量．

解答：解：设斜面的倾角为α，斜面的高度为h，释放点与停止位置间的距离为s，对全过程运用动能定理得，
mgh-μmgcosαs₁-μmgs₂=0
因为s₁cosα+s₂=s
整体得，mgh-μmgs=0
则μ=

h

s

．可知只要测量出初末位置的连线与水平方向的夹角，即可求出动摩擦因数．
实验时，将图钉固定于A、B两点，测出细线与水平方向的夹角θ，则μ=

h

s

．
故答案为：细线与木质轨道水平部分间的夹角θ，tanθ

点评：本题通过动能定理得出动摩擦因数的表达式，从而确定要测量的物理量．也可以通过动力学知识进行求解．