题目内容
 (2010?崇明县二模)如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉M瞬间,小球加速度的大小为12m/s2.若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是(取g=10m/s2)?( )
(2010?崇明县二模)如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉M瞬间,小球加速度的大小为12m/s2.若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是(取g=10m/s2)?( )分析:小球加速度的大小为12m/s2可能向上也可能向下,拔去销钉M瞬间,上面一个弹簧对小球的作用力为0,小球只受到下面弹簧的作用力,根据牛顿第二定律算出上面弹簧对小球的作用力,如拔去销钉N则下面一根弹簧作用力为0,再根据牛顿第二定律即可求解,要注意方向.
解答:解:设小球的质量为m,向上为正方向,刚开始受力平衡,则有:
FN+FM-G=0
拔去销钉M瞬间有:FN-G=±12m
所以FN=-2m或22m
所以FM=12m或-12m
去销钉N瞬间,小球受M弹簧和重力G的作用,
加速度为:a=
=2m/s2或-22m/s2
故选BC.
FN+FM-G=0
拔去销钉M瞬间有:FN-G=±12m
所以FN=-2m或22m
所以FM=12m或-12m
去销钉N瞬间,小球受M弹簧和重力G的作用,
加速度为:a=
| FN-G |
| m |
故选BC.
点评:本题主要考查了牛顿第二定律的应用,要求同学们能正确进行受力分析,注意加速度是矢量,难度不大.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 (2010?崇明县二模)在历史上关于重物和轻物坠落哪个快的问题,亚里斯多德和伽利略有不同的观点.如图所示的实验中,两端封闭的玻璃管称为“牛顿管”,将一个硬币和一根羽毛放在牛顿管中,让它们同时下落,如果在玻璃管中充满空气时,发现
(2010?崇明县二模)在历史上关于重物和轻物坠落哪个快的问题,亚里斯多德和伽利略有不同的观点.如图所示的实验中,两端封闭的玻璃管称为“牛顿管”,将一个硬币和一根羽毛放在牛顿管中,让它们同时下落,如果在玻璃管中充满空气时,发现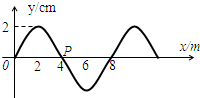 (2010?崇明县二模)如图所示为一列波在t=2.00s时刻的图象,P为波的传播方向上介质中的一点,波沿着x轴的正向传播,波速是40m/s,则下列说法正确的是( )
(2010?崇明县二模)如图所示为一列波在t=2.00s时刻的图象,P为波的传播方向上介质中的一点,波沿着x轴的正向传播,波速是40m/s,则下列说法正确的是( )