题目内容
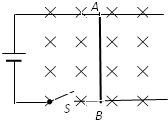 如图所示,电源的电动势E=1.5V,内电阻r=0.5Ω,AB=0.5m,AB电阻R=0.1Ω.固定框架的电阻不计.磁感应强度为0.5T.S闭合前AB静止.金属框对AB的滑动摩擦力为0.25N.
如图所示,电源的电动势E=1.5V,内电阻r=0.5Ω,AB=0.5m,AB电阻R=0.1Ω.固定框架的电阻不计.磁感应强度为0.5T.S闭合前AB静止.金属框对AB的滑动摩擦力为0.25N.(1)电键S闭合后,当AB的速度达到稳定时,电路中的电流多大?
(2)AB的最大速度多大?
(3)当AB速度达最大后,电源消耗的电能转化为什么形式的能?通过计算验证,能的转化是否符合守恒定律?
分析:以金属棒为研究对象,结合电路电流的变化,分析受力和运动情况,利用平衡态列方程;当速度稳定后,利用法拉第电磁感应定律求出感应电动势,找出等效电源,利用闭合电路的欧姆定律求解即可;据电路分别求出电阻消耗的热功率和摩擦生热与电源提供的功率比较.
解答:解:(1)以导体棒为研究对象,水平方向上受摩擦力和安培力,由于速度稳定后,所受合外力为零.
此时f=F=BIL
所以I=
=
A=1A
(2)设金属棒的最大速度为V,此时切割磁感线产生的电动势为E',据法拉第电磁感应定律得:E'=BLV…①
此时,该电路的等效电源的电动势为:E-E'
据闭合电路的欧姆定律得:I=
…②
联立①②代入数据解之得:V=3.6m/s
(3)导体AB速度达最大后,电源消耗的电能转化为回路的电热和AB与金属框摩擦产生的内能.
电源消耗的功率:
P=IE=1×1.5W=1.5W
回路产生的热功率:
P热=I2(R+r)=12×(0.1+0.5)W=0.6W
AB克服摩擦力做功的功率:
P'=fV=0.25×3.6W=0.9W
可知,P=P热+P'.
可见,能的转化符合守恒定律.
答:(1)电键S闭合后,当AB的速度达到稳定时,电路中的电流为1A.
(2)AB的最大速度3.6m/s
(3)当AB速度达最大后,电源消耗的电能通过摩擦力做功转化为内能和电流做功转化为热能.通过计算验证,能的转化是否符合守恒定律.
此时f=F=BIL
所以I=
| f |
| BL |
| 0.25 |
| 0.5×0.5 |
(2)设金属棒的最大速度为V,此时切割磁感线产生的电动势为E',据法拉第电磁感应定律得:E'=BLV…①
此时,该电路的等效电源的电动势为:E-E'
据闭合电路的欧姆定律得:I=
| E -E′ |
| R+r |
联立①②代入数据解之得:V=3.6m/s
(3)导体AB速度达最大后,电源消耗的电能转化为回路的电热和AB与金属框摩擦产生的内能.
电源消耗的功率:
P=IE=1×1.5W=1.5W
回路产生的热功率:
P热=I2(R+r)=12×(0.1+0.5)W=0.6W
AB克服摩擦力做功的功率:
P'=fV=0.25×3.6W=0.9W
可知,P=P热+P'.
可见,能的转化符合守恒定律.
答:(1)电键S闭合后,当AB的速度达到稳定时,电路中的电流为1A.
(2)AB的最大速度3.6m/s
(3)当AB速度达最大后,电源消耗的电能通过摩擦力做功转化为内能和电流做功转化为热能.通过计算验证,能的转化是否符合守恒定律.
点评:解题关键明确安培力与摩擦力相等时,金属棒达到稳定的速度,知道感应电动势是联系动力学和电学的纽带,灵活应用能量守恒.

练习册系列答案
相关题目
 如图所示,电源的电动势为50V,电源内阻为1.0Ω,定值电阻R=14Ω,M为直流电动机,电枢电阻R′=2.0Ω,电动机正常运转时,电压表读数为35V,求在100s时间内电源做的功和电动机上转化为机械能的部分是多少?
如图所示,电源的电动势为50V,电源内阻为1.0Ω,定值电阻R=14Ω,M为直流电动机,电枢电阻R′=2.0Ω,电动机正常运转时,电压表读数为35V,求在100s时间内电源做的功和电动机上转化为机械能的部分是多少?

