题目内容
如图11-3-14所示,M、N为两块带等量异种电荷的平行金属板,S1、S2为板上正对的小孔,N板右侧有两个宽度为d的匀强磁场区域,磁感应强度大小均为B,方向分别垂直于纸面向外和向里,磁场区域右侧有一个荧光屏.取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴,M板左侧电子枪发射出的热电子经小孔S1进入两板间,电子的质量为m,电荷量为e,初速度可以忽略.求:
(1)当两板间电势差为U0时,求从小孔S2射出的电子的速度v0.
(2)求两金属板间电势差U在什么范围内,电子不能穿过磁场区域而打到荧光屏上.
(3)若电子能够穿过磁场区域而打到荧光屏上,试定性地画出电子运动的轨迹.
(4)求电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系.

图11-3-14
(1)当两板间电势差为U0时,求从小孔S2射出的电子的速度v0.
(2)求两金属板间电势差U在什么范围内,电子不能穿过磁场区域而打到荧光屏上.
(3)若电子能够穿过磁场区域而打到荧光屏上,试定性地画出电子运动的轨迹.
(4)求电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系.

图11-3-14
(1)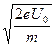 (2)U<
(2)U<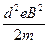 (3)见解析 (4)
(3)见解析 (4)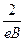
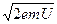 -
-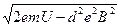 (U≥
(U≥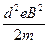 )
)
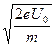 (2)U<
(2)U<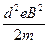 (3)见解析 (4)
(3)见解析 (4)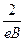
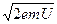 -
-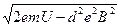 (U≥
(U≥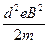 )
)(1)根据动能定理,得
eU0=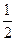 mv02
mv02
由此即可解得
v0=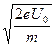 .
.
(2)欲使电子不能穿过磁场区域而打到荧光屏上,应有
r=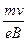 <d
<d
而eU=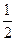 mv2
mv2
由此即可解得
U<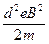 .
.
(3)电子穿过磁场区域而打到荧光屏上时运动的轨迹如图所示.
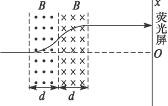
(4)若电子在磁场区域做圆周运动的轨道半径为r,穿过磁场区域打到荧光屏上的位置坐标为x,则由(3)中的轨迹图可得
x=2r-2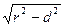
注意到r=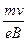 和eU=
和eU=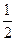 mv2
mv2
所以电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系为
x=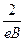 (
(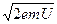 -
-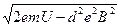 )(U≥
)(U≥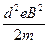 ).
).
eU0=
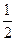 mv02
mv02由此即可解得
v0=
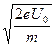 .
.(2)欲使电子不能穿过磁场区域而打到荧光屏上,应有
r=
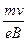 <d
<d而eU=
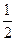 mv2
mv2由此即可解得
U<
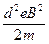 .
.(3)电子穿过磁场区域而打到荧光屏上时运动的轨迹如图所示.

(4)若电子在磁场区域做圆周运动的轨道半径为r,穿过磁场区域打到荧光屏上的位置坐标为x,则由(3)中的轨迹图可得
x=2r-2
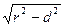
注意到r=
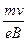 和eU=
和eU=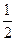 mv2
mv2所以电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系为
x=
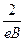 (
(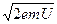 -
-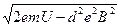 )(U≥
)(U≥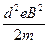 ).
).
练习册系列答案
相关题目
 粒子散射实验中发现了电子
粒子散射实验中发现了电子 )发生正碰。碰后产生两个新核,在磁场中形成如图14所示的两条半径分别为R和r (R>r)的圆形径迹。其中R是质量较小核的经迹,r是质量较大核的经迹。
)发生正碰。碰后产生两个新核,在磁场中形成如图14所示的两条半径分别为R和r (R>r)的圆形径迹。其中R是质量较小核的经迹,r是质量较大核的经迹。
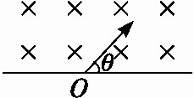

 .现垂直于圆轨道平面加一磁感强度为
.现垂直于圆轨道平面加一磁感强度为 的外磁场,这时电子的轨道半径没变,而它的速度发生了变化.若用
的外磁场,这时电子的轨道半径没变,而它的速度发生了变化.若用 表示此时环形电流在P点产生的磁感强度的大小,则当
表示此时环形电流在P点产生的磁感强度的大小,则当


