题目内容
7.水平道路上,一辆拖车通过一长度为L、不可伸长的轻绳的连接将另一辆故障车拖移.在拖车拉着故障车以v0=10m/s的速度匀速行驶过程中,拖车司机发现前方s=24m处有一障碍物,拖车司机立即开始刹车.刹车后故障c车做加速度大小为2m/s2的匀减速直线运动,拖车做加速度大小为a的匀减速直线运动(a可由拖车前机刹车力度控制)则:(1)为保证拖车不与障碍物碰撞,拖车的加速度a至少为多大;
(2)为保证拖车既不与障碍物碰撞,又不被后面的故障车撞上,试分析轻绳长度L需满足的条件及对应的a的取值范围.
分析 (1)根据拖车与障碍物的距离,结合速度位移公式求出拖车的最小加速度.
(2)根据速度位移公式求出故障车刹车到停下的距离,抓住刹车后故障车不与拖车相撞,结合位移关系求出加速度的范围,同时保证拖车不与障碍物相撞得出加速度的范围.结合加速度范围关系求出生成L需满足的条件.
解答 解:(1)设从开始刹车到停下,拖车的运动路程为s1,易知:${s}_{1}=\frac{{{v}_{0}}^{2}}{2a}$,
要保证拖车不与障碍物相碰,必须满足s1≤s,
代入数据解得$a≥\frac{25}{12}m/{s}^{2}$.
(2)设从开始刹车到完全停下,故障车的运动路程为s2,
易知:${s}_{2}=\frac{{{v}_{0}}^{2}}{2×2}=25m$,
要让刹车后故障车不与拖车相撞,应满足s2≤s1+L,代入解得$a≤\frac{50}{25-L}$,
而又要保证拖车不与障碍物相碰,必须满足s1≤s,即$a≥\frac{25}{12}m/{s}^{2}$,
综合可知a的范围为$\frac{25}{12}≤a≤\frac{50}{25-L}$,且此时要有$\frac{25}{12}≤\frac{50}{25-L}$与25-L>0,
即在上述a取值范围内的L满足1≤L≤25.
当L>25m时,有s2<L,即意味故障车一定不会撞上拖车,故此时只需保证拖车不撞上障碍物即可,即满足$\frac{25}{12}≤a$即可.
当L<1m时,一定会发生一种情况的碰撞.
答:(1)为保证拖车不与障碍物碰撞,拖车的加速度a至少为$\frac{25}{12}m/{s}^{2}$.
(2)L应满足1m≤L≤25m.a的取值范围为$\frac{25}{12}≤a≤\frac{50}{25-L}$.
点评 解决本题的关键理清拖车、故障车的运动规律,结合牛顿第二定律和运动学公式,抓住之间位移的关系进行求解.

| A. | 分析乒乓球的旋转 | B. | 研究地球自转时的地球 | ||
| C. | 研究车轮旋转情况时的车轮 | D. | 研究某同学从家到学校的速度 |
| A. | 物体速度的变化率越大,加速度就越大 | |
| B. | 物体速度的变化量越大,加速度就越大 | |
| C. | 物体的加速度方向一定与速度方向相同 | |
| D. | 物体的加速度方向与速度方向相反时,物体速度可能在增加 |
 宋代诗人陈与义乘着小船在风和日丽的春日出游曾写下了一首诗,其中的两旬是“卧看漫天云不动,不知云与我俱东”,表达了他对运动相对性的理解.诗中这两句涉及的参考系分别是( )
宋代诗人陈与义乘着小船在风和日丽的春日出游曾写下了一首诗,其中的两旬是“卧看漫天云不动,不知云与我俱东”,表达了他对运动相对性的理解.诗中这两句涉及的参考系分别是( )| A. | 岸和船 | B. | 船和岸 | C. | 都是岸 | D. | 都是船 |
| A. | F | B. | 2F | C. | $\frac{1}{2}$F | D. | $\frac{1}{4}$F |

| A. | b、c的线速度大小相等,且小于a的线速度 | |
| B. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| C. | a的周期大于c | |
| D. | a的向心力大于b |
 为了精确测量某待测电阻Rx的阻值(约为30Ω).有以下一些器材可供选择.
为了精确测量某待测电阻Rx的阻值(约为30Ω).有以下一些器材可供选择.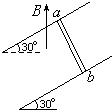 如图所示,放在平行光滑导轨上的导体棒ab质量为m,长为l,导轨所在平行面与水平面成30°角,导体棒与导轨垂直,空间有竖直向上的匀强磁场,磁感应强度为B,导体棒在导轨上处于静止状态,求:
如图所示,放在平行光滑导轨上的导体棒ab质量为m,长为l,导轨所在平行面与水平面成30°角,导体棒与导轨垂直,空间有竖直向上的匀强磁场,磁感应强度为B,导体棒在导轨上处于静止状态,求: