题目内容
如图，木块A放在木板B的左端，A、B间接触面粗糙，用恒力F将木块A拉到木板B的右端，第一次将B固定在水平地面上，第二次将B放在光滑水平地面上，则前后两个过程中相同的量是( )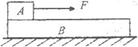
A．物块A运动的加速度
B．物块A的运动时间
C．力F对物块A做的功
D．系统产生的摩擦热量
AD
解析试题分析：设木块的质量为m，运动时间为t，位移为s1，木板的质量为M，位移为s2，长度为L，由于两次都能将木块A拉至木板B的右端，即总有：s1－s2＝L，因此，木块和木板间的摩擦两次都是滑动摩擦力，对木块，在水平方向上受拉力F和滑动摩擦力μmg，所以两次运动的加速度大小都为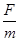
－μg，方向水平向右，故选项A正确；第一次木板固定，s2＝0，第二次B放在光滑水平地面上，s2＞0，所以第一次木块的位移比第二次的要小，故选项B错误；力F对物块A做的功为W＝Fs1，所以第一次力F对物块A做的功比第二次的小，故选项C错误；系统产生的摩擦热量Q＝FL，因此两次相等，故选项D正确。
考点：本题主要考查了物体的受力分析、牛顿运动定律、功的计算、功能关系的应用问题，属于中档题。
如图所示，一粗糙的水平传送带以恒定的速度v1沿顺时针方向运动，传送带的左、右两端皆有一与传送带等高的光滑水平面，一物体以恒定的速度v2沿水平面分别从左、右两端滑上传送带，下列说法正确的是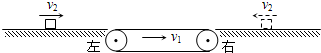
| A．物体从右端滑到左端所须的时间一定大于物体从左端滑到右端的时间 |
| B．若v2<v1，物体从左端滑上传送带必然先做加速运动，再做匀速运动 |
| C．若v2<v1，物体从右端滑上传送带，则物体可能到达左端 |
| D．若v2<v1，物体从右端滑上传送带又回到右端，在此过程中物体先做减速运动，再做加速运动 |
如图，两个质量分别为m1="3" kg、m2 = 2kg的物体置于光滑的水平面上，中间用轻质弹簧秤连接。两个大小分别为F1 =" 30" N、F2 =" 20" N的水平拉力分别作用在m1、m2上，则（ ）
| A．弹簧秤的示数是50N |
| B．弹簧秤的示数是24 N |
| C．在突然撤去F2的瞬间，m1的加速度大小为2 m/s2 |
| D．在突然撤去F2的瞬间，m2的加速度大小为12 m/s2 |
如图所示，有一个正方形的匀强磁场区域abcd，e是ad的中点，f是cd的中点，如果在a点沿对角线方向以速度v射入一带负电的带电粒子(带电粒子重力不计)，恰好从e点射出，则( )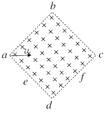
| A．如果粒子的速度增大为原来的二倍，将从d点射出 |
| B．如果粒子的速度增大为原来的三倍，将从f点射出 |
| C．如果粒子的速度不变，磁场的磁感应强度变为原来的二倍，也将从d点射出 |
| D．只改变粒子的速度使其分别从e、d、f点射出时，从e点射出所用时间最短 |
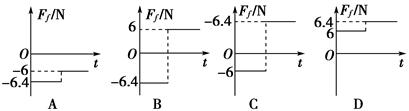
如图甲，某人正通过定滑轮将质量为m的货物提升到高处，滑轮的质量和摩擦均不计，货物获得的加速度
与绳子对货物竖直向上的拉力
之间的函数关系如图乙所示。由图可以判断： （ ） 
A．图线与纵轴的交点M的值 |
B．图线与横轴的交点N的值 |
| C．图线的斜率等于物体的质量m |
D．图线的斜率等于物体质量的倒数 |
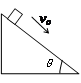
如图(a)所示，用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F，物体做变加速运动，其加速度a随外力F变化的图像如图(b)所示，若重力加速度g取10m/s2。根据图(b)中所提供的信息可以计算出
| A．加速度从2m/s2增加到6m/s2的过程中物体的速度变化量 |
| B．斜面的倾角 |
| C．物体的质量 |
| D．加速度为6m/s2时物体的速度 |
如图所示，斜面上除AB段粗糙外，其余部分均是光滑的，且物体与AB段动摩擦系数处处相同。今使物体（视为质点）由斜面顶端O处由静止开始下滑，经过A点时的速度与经过C点时的速度相等。AB=BC，则下列判断正确的是（ ）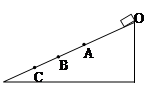
| A．物体在AB段与BC段的加速度相等 |
| B．物体在AB段与BC段的运动时间相等 |
| C．重力在这两段中所做功相等 |
| D．物体在AB段与BC段动量变化量相同 |