题目内容
 如图所示,皮带传动装置与水平面夹角为30°,两轮轴心相距L=3.8m,A、B分别是传送带与两轮的切点,轮缘与传送带之间不打滑,质量为0.1kg的小物块与传送带间的动摩擦因数为μ=
如图所示,皮带传动装置与水平面夹角为30°,两轮轴心相距L=3.8m,A、B分别是传送带与两轮的切点,轮缘与传送带之间不打滑,质量为0.1kg的小物块与传送带间的动摩擦因数为μ=
| ||
| 6 |
分析:根据牛顿第二定律和运动学公式分析小物块的运动情况.先由牛顿第二定律求出小物块沿传送带向下匀加速运动的加速度,由运动学公式求出物块速度与传送带相等时所经过的时间和通过的位移,判断物块的速度与传动带速度相等以后物体的运动情况,再根据牛顿第二定律和运动学公式结合求解;小物块相对于传送带运动时,在传送带上留下痕迹等于两者相对路程的大小.分析传送带速度与留下的痕迹长度的关系,产生的热量等于滑动摩擦力做的功.
解答:解:A、小物块受到竖直向下的重力、垂直传送带向上的支持力和沿传送带斜向下的摩擦力作用,做匀加速直线运动,设加速度为a1,根据牛顿第二定律有:
mgsin30°+μmgcos30°=ma1
解得:a1=7.5m/s2,故A错误;
当小物块速度等于3m/s时,设小物块对地位移为L1,用时为t1,根据匀加速直线运动规律得:
t1=
=
=0.4s
L1=
at2=
×7.5×0.16=0.6m
由于L1<L 且μ<tan30°,当小物块速度等于3m/s时,小物块将继续做匀加速直线运动至B点,设
加速度为a2,用时为t2,根据牛顿第二定律和匀加速直线运动规律得:
mgsin30°-μmgcos30°=ma2
解得:a2=2.5m/s2
又L-L1=v1t2+
a2t22
解得:t2=0.8 s
物块到B点的速度为:v2=v1+a2t2=3+2.5×0.8=5m/s
整个过程中对A运用动能定理得:
mv2=mgLsin30°+W
解得:W=
×0.1×25-0.1×10×3.8×
=-0.65J,故B错误;
C、第一阶段,传送带的位移为:x1=v1t1=3×0.4=1.2m
相对位移△x1=x1-L1=1.2-0.6=0.6m
第二阶段,传送带位移为:x2=v1t2=3×0.8=2.4m
相对位移为:△x2=x2-(L-L1)=3.2-2.4=0.8m,
第一阶段传送带速度比物体快,第二阶段物体比传送带快,所以小物块在传送带上留下的痕迹长度0.8m,故C正确;
D、摩擦力做的功为:W=f(△x1+△x2)=μmgcosθ(△x1+△x2)=
×0.1×10×
×1.4=0.35J,所以整个过程中小物块与传送带因摩擦而产生的热量0.35J,故D错误.
故选:C
mgsin30°+μmgcos30°=ma1
解得:a1=7.5m/s2,故A错误;
当小物块速度等于3m/s时,设小物块对地位移为L1,用时为t1,根据匀加速直线运动规律得:
t1=
| v |
| a1 |
| 3 |
| 7.5 |
L1=
| 1 |
| 2 |
| 1 |
| 2 |
由于L1<L 且μ<tan30°,当小物块速度等于3m/s时,小物块将继续做匀加速直线运动至B点,设
加速度为a2,用时为t2,根据牛顿第二定律和匀加速直线运动规律得:
mgsin30°-μmgcos30°=ma2
解得:a2=2.5m/s2
又L-L1=v1t2+
| 1 |
| 2 |
解得:t2=0.8 s
物块到B点的速度为:v2=v1+a2t2=3+2.5×0.8=5m/s
整个过程中对A运用动能定理得:
| 1 |
| 2 |
解得:W=
| 1 |
| 2 |
| 1 |
| 2 |
C、第一阶段,传送带的位移为:x1=v1t1=3×0.4=1.2m
相对位移△x1=x1-L1=1.2-0.6=0.6m
第二阶段,传送带位移为:x2=v1t2=3×0.8=2.4m
相对位移为:△x2=x2-(L-L1)=3.2-2.4=0.8m,
第一阶段传送带速度比物体快,第二阶段物体比传送带快,所以小物块在传送带上留下的痕迹长度0.8m,故C正确;
D、摩擦力做的功为:W=f(△x1+△x2)=μmgcosθ(△x1+△x2)=
| ||
| 6 |
| ||
| 2 |
故选:C
点评:本题的关键之处在于分析物块的运动情况,也可以通过作速度图象分析.

练习册系列答案
相关题目
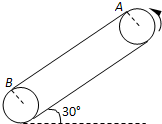 如图所示,皮带传动装置与水平面夹角为30°,轮半径R=
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=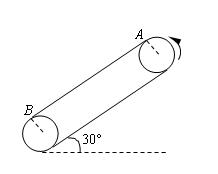
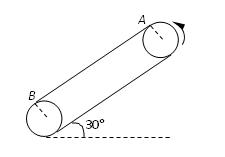
 m,两轮轴心相距L=3.75m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑。一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=
m,两轮轴心相距L=3.75m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑。一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ= 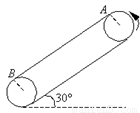
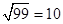 )
)