题目内容
我国“玉兔号”月球车被顺利送抵月球表面，并发回大量图片和信息．若该月球车在地球表面的重力为G1，在月球表面的重力为G2．已知地球半径为R1，月球半径为R2，地球表面处的重力加速度为g，则（ ）
A、“玉兔号”月球车在地球表面与月球表面质量之比为
| ||||||
B、地球的质量与月球的质量之比为
| ||||||
C、地球表面处的重力加速度与月球表面处的重力加速度之比为
| ||||||
D、地球的第一宇宙速度与月球的第一宇宙速度之比为
|
练习册系列答案
应用题作业本系列答案
相关题目
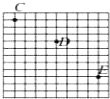如图所示是小球做平抛运动的闪光照片，照片中的每个正方形小格的边长代表的实际长度为5.0cm．己知闪光频率是10Hz．则根据上述的信息下列说法正确的是（ ）| A、当地的重力加速度大小为9.80m/s2 | ||
| B、小球平抛的初速度大小为2.0m/s | ||
C、C小球在D点时速度大小为
| ||
D、小球到达E点时的速度方向与水平方向夹角的正切值为
|
杂技演员驾驶摩托车表演“飞车走壁”其简化后的模型如图所示，表演者沿表演台的侧壁做匀速圆周运动．若表演时杂技演员和摩托车的总质量不变，摩托车与侧壁间沿侧壁倾斜方向的摩擦力恰好为零，轨道平面离地面的高度为H，侧壁倾斜角度α不变，则下列说法中正确的是（ ）| A、摩托车做圆周运动的H越高，角速度越大 | B、摩托车做圆周运动的H越高，线速度越小 | C、侧壁对摩托车提供的向心力随高度H变大而减小 | D、侧壁对摩托车提供的向心力不随H的变化而变化 |
“嫦娥三号”卫星在距月球100公里的圆形轨道上开展科学探测，其飞行的周期为118分钟，若已知月球半径和万有引力常量，由此可推算（ ）
| A、“嫦娥三号”卫星绕月运行的速度 | B、“嫦娥三号”卫星的质量 | C、月球对“嫦娥三号”卫星的吸引力 | D、月球的质量 |
一宇宙飞船绕地心做半径为r的匀速圆周运动，飞船舱内有一质量为m的人站在可称体重的台秤上．用R表示地球的半径，g表示地球表面处的重力加速度，g′表示宇宙飞船所在处的地球引力加速度，FN表示人对秤的压力，下面说法中正确的是（ ）
A、g′=
| ||
B、g′=
| ||
C、FN=m
| ||
D、FN=m
|
质量不等的两星体在相互间的万有引力作用下，绕两者连线上某一定点O做匀速圆周运动，构成双星系统．由天文观察测得其运动周期为L两星体之间的距离为r，已知引力常量为G．下列说法正确的是（ ）
A、双星系统的平均密度为
| ||
| B、D点离质量较大的星体较远 | ||
C、双星系统的总质量为
| ||
| D、若在D点放一物体，则物体受两星体的万有引力合力为零 |
“嫦娥”三号探测器发射到月球上要经过多次变轨，最终降落到月球表面上，其中轨道Ⅱ为圆形．下列说法正确的是（ ）| A、探测器在轨道Ⅱ上运动时不需要火箭提供动力 | B、探测器在轨道Ⅲ经过P点时的加速度小于在轨道Ⅱ经过P时的加速度 | C、探测器在P点由轨道Ⅱ进入轨道Ⅲ必须加速 | D、轨道Ⅱ是月球卫星绕月球做匀速圆周运动的唯一轨道 |
如果把水星和金星绕太阳的轨道视为圆周，从水星与金星在一条直线上开始计时，若测得在相同时间内水星、金星转过的角度分别为θ1、θ2（均为锐角），则由此条件可求得水星和金星（ ）| A、质量之比 | B、绕太阳的动能之比 | C、到太阳的距离之比 | D、受到的太阳引力之比 |
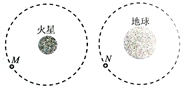火星的质量是地球质量的| 1 |
| 9 |
A、火星表面的重力加速度是地球的
| ||
B、卫星M的向心加速度是卫星N的
| ||
| C、卫星M和卫星N的线速度大小相等 | ||
| D、卫星M的运行周期是卫星N的3倍 |