题目内容
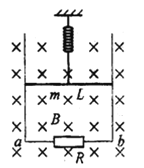
【题目】两根足够长的间距为L的光滑导轨竖直固定,底端接阻值为R的电阻,将阻值也为R金属棒悬挂在一固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,如图所示。导轨电阻不计,重力加速度为g。现将金属棒从弹簧原长位置由静止释放,则( )
A、释放瞬间金属棒的加速度一定等于g
B、金属棒到达最低点的加速度一定等于g
C、电路上产生的总热量可能等于金属棒重力势能的减少量
D、金属棒的速度为v时,电阻R的电功率为![]()
【答案】AD
【解析】
试题分析:金属棒在释放的瞬间,速度为零,不产生感应电动势和感应电流,不受安培力的作用,只受到重力,因此释放瞬间金属棒的加速度一定等于![]() ,故A正确;若没有磁场,金属棒做简谐运动,根据对称性可知金属棒到达最低点的加速度大小一定等于g,而现在金属棒在磁场中运动时,受到安培阻力作用,金属棒在最低点时弹簧伸长的长度比没有磁场时要短,弹力要小,根据牛顿第二定律可知加速度一定小于
,故A正确;若没有磁场,金属棒做简谐运动,根据对称性可知金属棒到达最低点的加速度大小一定等于g,而现在金属棒在磁场中运动时,受到安培阻力作用,金属棒在最低点时弹簧伸长的长度比没有磁场时要短,弹力要小,根据牛顿第二定律可知加速度一定小于![]() ,故B错误;在金属棒运动的过程中,电阻R上产生的总热量等于棒的重力势能减少量与弹簧的弹性势能增加量之差,故C错误;当金属棒的速度为v时,产生的感应电动势为
,故B错误;在金属棒运动的过程中,电阻R上产生的总热量等于棒的重力势能减少量与弹簧的弹性势能增加量之差,故C错误;当金属棒的速度为v时,产生的感应电动势为![]() ,回路中的电流为
,回路中的电流为![]() ,电阻R的电功率为
,电阻R的电功率为![]() ,联立得
,联立得![]() ,故D正确。
,故D正确。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】用某单色光做光的双缝干涉实验,能在光屏上观察到干涉条纹。若把其中一条缝遮住,则在光屏上( )
A. 没有任何条纹
B. 只有一条亮条纹
C. 有等间距的明暗相间的条纹
D. 有不等间距的明暗相间的条纹