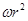题目内容
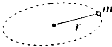 如图所示,一个小球绕圆心O做匀速圆周运动,圆周半径为r,小球运动的线速度为v,则它运动的加速度a为( )
如图所示,一个小球绕圆心O做匀速圆周运动,圆周半径为r,小球运动的线速度为v,则它运动的加速度a为( )| A、ω2r | ||
| B、ωr | ||
C、
| ||
| D、ωr2 |
分析:已知小球做匀速圆周运动,知道了小球的圆周运动半径r和角速度ω,即可求出线速度根据向心加速度的公式表示出加速度.
解答:解:小球的半径r和角速度ω为已知,则小球的线速度大小为:v=ωr.
根据向心加速度公式a=
得:a=ω2r.
那么,选项A正确,选项B、C、D错误.
故选:A.
根据向心加速度公式a=
| v2 |
| r |
那么,选项A正确,选项B、C、D错误.
故选:A.
点评:熟记描述匀速圆周运动的物理量线速度、角速度、周期、转速等之间的关系,即v=ωr,v=
或ω=
等.
| 2πr |
| T |
| 2π |
| T |

练习册系列答案
相关题目
 如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度大小为ω,则它运动线速度的大小为( )
如图所示,一个小球绕圆心O做匀速圆周运动,已知圆周半径为r,该小球运动的角速度大小为ω,则它运动线速度的大小为( )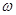 ,则它运动线速度的大小为
,则它运动线速度的大小为




 ,则它运动线速度的大小为
,则它运动线速度的大小为
 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.