题目内容
【题目】如图所示,光滑圆形轨道固定在竖直平面内,一可视为质点的小球在轨道内运动,小球始终不脱离轨道,重力加速度为g。则小球通过最低点时的加速度大小不可能为( )
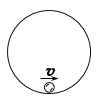
A. ![]() B.
B. ![]() C. 2g D. 3g
C. 2g D. 3g
【答案】D
【解析】
球在轨道内运动,小球始终不脱离轨道,分完整的圆周运动和小角度摆动两种情况:(1)如果是完整的圆周运动,最高点速度最小时重力提供向心力,根据牛顿第二定律得到最小速度;小球运动过程中机械能守恒,根据机械能守恒定律得到最低点速度,根据向心加速度公式得到最低点的向心加速度。(2)如果是小角度摆动,小球的最高点是上升到与圆心等高。
情况一:完整的圆周运动
球在最高点是重力和支持力的合力提供向心力,支持力为零时速度最小,根据牛顿第二定律,有:![]()
解得:![]()
从最高点到最低点过程,以最低点为零势能参考点,根据机械能守恒定律,有:
![]()
解得:![]()
故最低点的最小加速度为:![]() ;
;
情况二:不完整的圆周运动
如果是小角度摆动,最低点速度最大时运动的最高点与圆心等高,以最低点为零势能参考点,根据机械能守恒定律,有:![]()
解得:![]()
最低点向心加速度的最大值为:![]()
综上,最低点的向心加速度的单位为:a≤2g,或者a≥5g;
故选:D。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目