题目内容
10. 如图所示,质量为m=2kg的木块在倾角为370的斜面上由静止开始下滑,木块与斜面间的动摩擦因数为0.5,已知g=10m/s2,求:
如图所示,质量为m=2kg的木块在倾角为370的斜面上由静止开始下滑,木块与斜面间的动摩擦因数为0.5,已知g=10m/s2,求:(1)前2s内重力做的功.
(2)第3s内重力的平均功率.
(3)第4s末重力的瞬时功率.
分析 根据牛顿第二定律求出木块的加速度,结合位移时间公式求出位移的大小,从而求出重力做功的大小,结合平均功率和瞬时功率的公式求出重力的平均功率和瞬时功率.
解答 解:(1)根据牛顿第二定律得,木块的加速度a=$\frac{mgsin37°-μmgcos37°}{m}$=gsin37°-μgcos37°=6-0.5×8m/s2=2m/s2,
2s内的位移x=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×2×4m=4m$
则前2s内重力做功WG=mgxsin37°=20×4×0.6J=48J,
(2)第3s内的位移$x′=\frac{1}{2}a{{t}_{3}}^{2}-\frac{1}{2}a{{t}_{2}}^{2}=\frac{1}{2}×2×(9-4)m=5m$,
则重力做功的平均功率$\overline{P}=\frac{mgx′sin37°}{t}=\frac{20×5×0.6}{1}W=60W$.
(3)4s末的速度v=at4=2×4m/s=8m/s,则重力的瞬时功率P=mgvsin37°=20×8×0.6W=96W.
答:(1)前2s内重力做的功为48J.
(2)第3s内重力的平均功率为60W.
(3)第4s末重力的瞬时功率为96W.
点评 本题考查了牛顿第二定律、运动学公式、功率的基本运用,知道平均功率和瞬时功率的区别,掌握这两种功率的求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列说法正确的是( )
| A. | 结合能越大的原子核,原子核中的核子结合得越牢固,原子核越稳定 | |
| B. | 较轻的原子核和较重的原子核的比结合能比中等大小原子核的比结合能要小,在重核裂变反应和轻核聚变反应中都会出现质量亏损的现象 | |
| C. | 核力是强相互作用的一种表现,在原子核的尺度内,核力比库伦力大得多,在原子的尺度内,电磁力比核力要大,核力是短程力 | |
| D. | 目前,人类已经可以做到稳定地输出聚变能,所以人类不再有“能源危机” |
1.如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,电流表、电压表均为理想电表,R是光敏电阻(其阻值随光强增大而减小).原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )
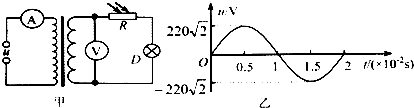
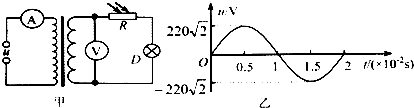
| A. | 电压u的频率为5Hz | |
| B. | 电压表的示数为22V | |
| C. | 照射R的光变强时,灯泡变暗 | |
| D. | 照射R的光变强时,电流表的示数变大 |
18. 如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
 如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )| A. | 交流电a的瞬时值为μ=10sin5πtV | |
| B. | 线圈先后两次转速之比为2:3 | |
| C. | 交流电b电压的有效值为$\frac{20}{3}$V | |
| D. | 在t=0时刻穿过线圈的磁通量变化率均为零 |
5.如图所示,小车M在恒力F作用下,沿水平地面做直线运动,由此可判断( )


| A. | 若地面光滑,则小车一定受三个力作用 | |
| B. | 若地面粗糙,则小车可能受三个力作用 | |
| C. | 若小车做匀速运动,则小车一定受四个力的作用 | |
| D. | 若小车做匀速运动,则小车可能受三个力的作用 |
19. 如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
 如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )
如图,两根光滑金属导轨平行放置,导轨所在平面与水平面间的夹角为θ,整个装置处于垂直于导轨平面方向的匀强磁场中.质量为m的金属杆ab垂直导轨放置,当杆中通从a 到b的电流I时,ab刚好静止.则( )| A. | 磁场方向垂直于导轨平面向下 | B. | 磁场方向垂直于导轨平面向上 | ||
| C. | ab受安培力的大小等于mgsinθ | D. | ab受安培力的大小等于mgtanθ |
 如图所示,小球a、b用等长细线悬挂于同一固定点O.让小球a静止下垂,将小球b向右拉起,使细线水平,已知细线长为L,小球a、b的质量分别为2m和m,在小球a上固定有极少量火药,由静止释放小球b,两球碰撞后火药会发生爆炸而使两小球相互分开,此后观察到系小球a的细线与竖直方向的最大偏角为90°.忽略空气阻力,重力加速度为g,求:
如图所示,小球a、b用等长细线悬挂于同一固定点O.让小球a静止下垂,将小球b向右拉起,使细线水平,已知细线长为L,小球a、b的质量分别为2m和m,在小球a上固定有极少量火药,由静止释放小球b,两球碰撞后火药会发生爆炸而使两小球相互分开,此后观察到系小球a的细线与竖直方向的最大偏角为90°.忽略空气阻力,重力加速度为g,求: