��Ŀ����
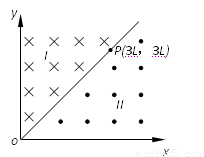
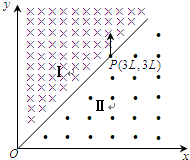 ��ͼ��ʾ���ڿռ�����һ����ϵoxy�����һ�����г�������������ͬ����ǿ�ų������͢�ֱ��OP�����ǵı߽磮������еĴŸ�Ӧǿ��Ϊ2B������ֱֽ�����ڣ�������еĴŸ�Ӧǿ��ΪB������ֱֽ�����⣬�߽��ϵ�P������Ϊ��3L��3L����һ����Ϊm�������Ϊ+q�����Ӵ�P��ƽ����y�����������ٶ�v0=
��ͼ��ʾ���ڿռ�����һ����ϵoxy�����һ�����г�������������ͬ����ǿ�ų������͢�ֱ��OP�����ǵı߽磮������еĴŸ�Ӧǿ��Ϊ2B������ֱֽ�����ڣ�������еĴŸ�Ӧǿ��ΪB������ֱֽ�����⣬�߽��ϵ�P������Ϊ��3L��3L����һ����Ϊm�������Ϊ+q�����Ӵ�P��ƽ����y�����������ٶ�v0=| 2BqL | m |
��1�������ڢ�͢����ų�����Բ���˶��İ뾶֮�ȣ�
��2�������ڴų����˶�����ʱ�估�뿪�ų���λ�����꣮
��������1��������������ų��У������������ṩ��������������Բ���˶�����ţ�ٵڶ����ɺ���������ʽ��뾶�����õ��뾶֮�ȣ�
��2����Բ���˶�֪ʶ�õ����ڹ�ʽT=
���������������ת����Բ�Ľ�Ϊ��1=
������������������˶���ʱ��Ϊt1=
T1���������������ת����Բ�Ľ�Ϊ��2=
����������������˶���ʱ��Ϊt2=
T2�����������ʱ�䣮
��v0=
����뾶��ʽR=
���õ������������ų���Բ���˶��İ뾶���ɼ��ι�ϵ��������뿪�ų���λ�����꣮
��2����Բ���˶�֪ʶ�õ����ڹ�ʽT=
| 2��m |
| qB |
| 3 |
| 2 |
| ��1 |
| 2�� |
| �� |
| 2 |
| ��2 |
| 2�� |
��v0=
| 2BqL |
| m |
| mv |
| qB |
����⣺��1��������������ų��У������������ṩ��������������Բ���˶�������ţ�ٵڶ����ɵ�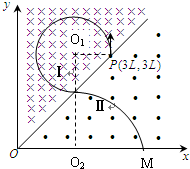
qvB=m
��
��� R=
��
���ԣ������ڢ�͢����ų�����Բ���˶��İ뾶�ֱ�Ϊ��R1=
��R2=
��
���
=
��
��2�������ڴų���Բ���˶�������ΪT=
��
�ɵ� T1=
��T2=
��
�������������ת����Բ�Ľ�Ϊ��1=
�� ��
��������������˶���ʱ��Ϊt1=
T1 ��
���t1=
��
�������������ת����Բ�Ľ�Ϊ��2=
��
��������������˶���ʱ��Ϊt2=
T2 ��11��
���t2=
��12��
����t=t1+t2=
��13��
���ٶ�v0=
�����
R1=L��R2=2L ��14��
�ɼ��ι�ϵ��
=3L-R1��
=R2 ��15��
�����뿪�ų��ĺ�����Ϊx=
+
=4L ��16��
�����뿪�ų���λ�����꣨4L��0����17��
�𣺣�1�������ڢ�͢����ų�����Բ���˶��İ뾶֮����1��2��
��2�������ڴų����˶�����ʱ����
���뿪�ų���λ�������ǣ�4L��0����

qvB=m
| v2 |
| R |
��� R=
| mv |
| qB |
���ԣ������ڢ�͢����ų�����Բ���˶��İ뾶�ֱ�Ϊ��R1=
| mv0 |
| 2qB |
| mv0 |
| qB |
���
| R1 |
| R2 |
| 1 |
| 2 |
��2�������ڴų���Բ���˶�������ΪT=
| 2��m |
| qB |
�ɵ� T1=
| ��m |
| qB |
| 2��m |
| qB |
�������������ת����Բ�Ľ�Ϊ��1=
| 3 |
| 2 |
��������������˶���ʱ��Ϊt1=
| ��1 |
| 2�� |
���t1=
| 3��m |
| 4qB |
�������������ת����Բ�Ľ�Ϊ��2=
| �� |
| 2 |
��������������˶���ʱ��Ϊt2=
| ��2 |
| 2�� |
���t2=
| ��m |
| 2qB |
����t=t1+t2=
| 5��m |
| 4qB |
���ٶ�v0=
| 2BqL |
| m |
R1=L��R2=2L ��14��
�ɼ��ι�ϵ��
. |
| OO2 |
. |
| O2M |
�����뿪�ų��ĺ�����Ϊx=
. |
| OO2 |
. |
| O2M |
�����뿪�ų���λ�����꣨4L��0����17��
�𣺣�1�������ڢ�͢����ų�����Բ���˶��İ뾶֮����1��2��
��2�������ڴų����˶�����ʱ����
| 5��m |
| 4qB |
�����������������ڴų�������Բ���˶������⣮�ڴų���Բ���˶����÷����ǻ��켣���ɼ���֪ʶ��뾶��

��ϰ��ϵ�д�
�����Ŀ

 ��������I��������Iƫת���������II��������������������
��������I��������Iƫת���������II��������������������
 ��������I��������Iƫת���������II��������������������
��������I��������Iƫת���������II��������������������