题目内容
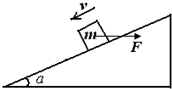如图所示，在倾角为a的斜面上，放着一质量为m的滑块，现用水平推力F作用在滑块上，使滑块匀速下滑，斜面保持静止，求：（1）滑块与斜面间的动摩擦因数μ
（2）假设斜面质量为M，且斜面和地之间的动摩擦因数与斜面和滑块之间的动摩擦因数相等，求斜面受到的地面的摩擦力
（3）斜面对滑块的作用力为多大？方向如何？（可用三角函数表示）
分析：（1）由受力平衡可以得到一个沿斜面的平衡方程，由此可以求的摩擦因数
（2）整体法分析可以知道，斜面受到的地面摩擦力就等于推力F
（3）斜面对滑块的作用力由两部分，一是摩擦力，二是支持力，两者合力为斜面对滑块的作用力
（2）整体法分析可以知道，斜面受到的地面摩擦力就等于推力F
（3）斜面对滑块的作用力由两部分，一是摩擦力，二是支持力，两者合力为斜面对滑块的作用力
解答：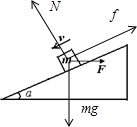
解：
（1）滑块受力如图：
故有：mgsinα-Fcosα-μmgcosα=0
解得：
μ=
=tanα-
（2）整体法分析可以知道，整体在水平方向只受推力F和地面的摩擦力，因整体是受力平衡的，故斜面受到的地面摩擦力就等于推力F
（3）由受力图可知，斜面对滑块的作用力F0应等于重力与推力的合力，故
F0=
方向为：
tanθ=
答：
（1）滑块与斜面间的动摩擦因数μ=tanα-
（2）斜面受到的地面的摩擦力F
（3）斜面对滑块的作用力为
； 方向为：tanθ=
．
解：（1）滑块受力如图：
故有：mgsinα-Fcosα-μmgcosα=0
解得：
μ=
| mgsinα-Fcosα |
| mgcosα |
| F |
| mg |
（2）整体法分析可以知道，整体在水平方向只受推力F和地面的摩擦力，因整体是受力平衡的，故斜面受到的地面摩擦力就等于推力F
（3）由受力图可知，斜面对滑块的作用力F0应等于重力与推力的合力，故
F0=
| F2+mg2 |
方向为：
tanθ=
| F |
| mg |
答：
（1）滑块与斜面间的动摩擦因数μ=tanα-
| F |
| mg |
（2）斜面受到的地面的摩擦力F
（3）斜面对滑块的作用力为
| F2+mg2 |
| F |
| mg |
点评：灵活应用受力分析的方法，整体法与部分法的应用非常重要．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
（2011?杭州一模）如图所示，在倾角为a的光滑斜面上，垂直纸面放置一根长为L，质量为m的直导体棒．当导体棒中的电流I垂直纸面向里时，欲使导体棒静止在斜面上，可加一平行于纸面的匀强磁场，当外加匀强磁场的磁感应强度B的方向由垂直斜面向上沿逆时针转至水平向左的过程中，下列关于B的大小变化的说法中，正确的是（ ）
（2010?南昌一模）如图所示，在倾角为a的传送带上有质量均为m的三个木块1、2，3，中间均用原长为L，劲度系数为k的轻弹簧连接起来，木块与传送带间的动摩擦因数均为μ，其中木块1被与传送带平行的细线拉住，传送带按图示方向匀速运行，三个木块处于平衡状态．下列结论正确的是（ ）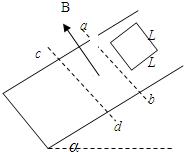
如图所示，在倾角为a的光滑斜面上，abcd区域存在着垂直斜面向上的匀强磁场，边界ab和cd都沿水平方向，ac=L，在斜面上质量为m，边长为L的正方形导线框沿斜面自由下滑，恰好匀速穿过磁场，下列说法正确的是（ ）