题目内容
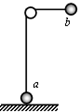（2009?青浦区一模）如图，一根跨越一固定水平光滑细杆的轻绳，两端各系一个小球，球a置于地面，球b被拉到与细杆同一水平的位置．在绳刚被拉直时，球b从静止状态向下摆动，当球b摆到竖直位置时，球a刚要离开地面，则两球质量之比ma：mb为（ ）分析：当b球摆到竖直最低位置时，a球刚要离开地面．则绳子的拉力大小等于a球的重力．由牛顿第二定律，结合向心力公式可列出质量、速度及半径间的关系；再运用机械能守恒定律可列出b球的质量与速度间的关系；最后可求出两球质量关系．
解答：解：小球b从静止摆到最低位置的过程中，仅有重力做功，所以小球机械能守恒．
则有：
mbv2-0=mbgh （1）
小球b最低位置受力分析：重力、拉力；运动分析：圆周运动，
则有：T-mbg=mb
（2）
小球b摆到最低位置时，小球a刚要离开地面．
则有：T=mag （3）
由（1）（2）（3）可得：ma：mb=3：1
故选为C
则有：
| 1 |
| 2 |
小球b最低位置受力分析：重力、拉力；运动分析：圆周运动，
则有：T-mbg=mb
| v2 |
| h |
小球b摆到最低位置时，小球a刚要离开地面．
则有：T=mag （3）
由（1）（2）（3）可得：ma：mb=3：1
故选为C
点评：小球b在下摆过程中运用机械能守恒定律，在最低点运用牛顿第二定律．同时借助于小球a 的重力得知小球b摆到最低点时绳子的拉力大小，从而将两球质量联系起来．
练习册系列答案
相关题目
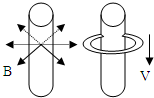（2009?青浦区一模）如图，一个很长的竖直放置的圆柱形磁铁，产生一个辐射状的磁场（磁场水平向外），其大小为B=K/r，r为半径，设一个与磁铁同轴的圆形铝环，半径为R（大于圆柱形磁铁半径），而弯成铝环的铝丝其截面积为S，铝丝电阻率为ρ，密度为ρ0．铝环通过磁场由静止开始下落，下落过程中铝环平面始终保持水平．试求：
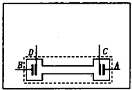（2009?青浦区一模）如图所示，是一种内电阻可调的化学电池，可用来验证闭合电路欧姆定律．A、B为电池的正、负极，C、D为靠近正、负极板的两个探极，目的是为了测量电池的内部电压．向电池内打气，可以改变电解质溶液液面的高低，从而改变电池的内电阻．
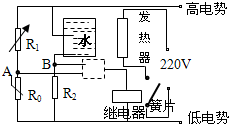（2009?青浦区一模）如图所示的是热水器的恒温集成电路，R0是热敏电阻，温度较低时的阻值很大，温度较高时的阻值很小．如果热水器中没有水或水温较高时，继电器会放开簧片，发热器断路，反之会吸住簧片接通发热器．则在电路的虚线框内的门电路应是