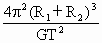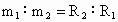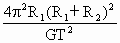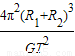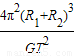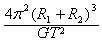题目内容
宇宙中两颗相距很近的恒星常常组成一个双星系统，它们以相互间的万有引力彼此提供向心力，从而使它们绕着某一共同的圆心做匀速圆周运动，若已知它们的运转周期为T，两星到某一共同圆心的距离分别为R1和R2，那么，双星系统中两颗恒星的质量关系（ ）
分析：由双星系统两个星体受的万有引力相等，故有此可以求得各自的质量表达式，以及质量之比．
解答：解：
A：对m1有：G
=m1R1
，解得：m2=
，同理可得：m1=
，故两者质量不相等，故A错误
B：由A两者质量相加得：
，故B正确
C：由A知m1：m2=R2：R1故C正确．
D：由C知，两者质量之和为
，则不可能其中一个的质量为
，故D错误
故选BC
A：对m1有：G
| m1m2 |
| (R1+R2)2 |
| 4π2 |
| T2 |
| 4π2R1(R1+R2)2 |
| GT2 |
| 4π2R2(R1+R2)2 |
| GT2 |
B：由A两者质量相加得：
| 4π2(R1+R2)3 |
| GT2 |
C：由A知m1：m2=R2：R1故C正确．
D：由C知，两者质量之和为
| 4π2(R1+R2)3 |
| GT2 |
| 4π2(R1+R2)3 |
| GT2 |
故选BC
点评：本题主要是依据双星的两个共同量：引力和周期，来列相应的表达式，进而才能解得需要的结果．这两个共同量一般是解决双星问题的关键．
练习册系列答案
相关题目
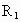和
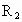，那么，关于这双星系统中两颗恒星的质量关系的说法不正确的是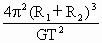
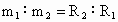
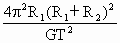
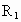和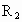
，那么，关于这双星系统中两颗恒星的质量关系的说法不正确的是
