题目内容
20世纪20年代,剑桥大学学生G·泰勒做了一个实验,在一个密闭的箱子里放上小灯泡、烟熏黑的玻璃、狭缝、针尖、照相底片,整个装置如图
图
(1)假设起作用的光波长约为500 nm,计算从一个光子到来和下一光子到来所相隔的平均时间,及光束中两邻近光子之间的平均距离.
(2)如果当时实验用的箱子长为
解析:每秒到达底片的能量与每个光子的能量的比值就是每秒到达底片的光子数,认为光子是依次到达底片的,根据时间间隔,可计算出光子间的平均距离.
(1)对于λ=500 nm的光子能量为
E=hν=h![]() =6.63×10-34×
=6.63×10-34×![]() J=4.0×1019 J
J=4.0×1019 J
因此每秒到达底片的光子数为
n=![]() =
=![]() =1.25×106(个)
=1.25×106(个)
如果光子是依次到达底片的,则光束中相邻两光子到达底片的时间间隔是:
Δt=![]() s=
s=![]() s=8×10-7 s
s=8×10-7 s
故相邻两个光子间平均距离为:
d=cΔt=3.0×108×8×10
(2)由(1)的计算结果可知,两光子间距有2.4×

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
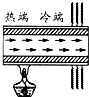 “热管”是20世纪80年代研制出来的一种导热本领非常大的装置.它比铜的导热本领大上千倍.“热管”的结构并不复杂,它是一根两端封闭的合金管,管内壁衬了一层多孔的材料,叫做吸收芯,吸收芯中充有酒精或其他易汽化的液体,如图所示,当管的一端受热时,热量会很快传到另一端,试分析其中的道理.
“热管”是20世纪80年代研制出来的一种导热本领非常大的装置.它比铜的导热本领大上千倍.“热管”的结构并不复杂,它是一根两端封闭的合金管,管内壁衬了一层多孔的材料,叫做吸收芯,吸收芯中充有酒精或其他易汽化的液体,如图所示,当管的一端受热时,热量会很快传到另一端,试分析其中的道理.