Question

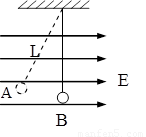
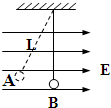如图，水平匀强电场的电场强度为E，一个带电小球质量为m，轻质的绝缘细线长为L，静止时小球位于A点，细线与竖直方向成30°角，求：
（1）小球带何种电荷？电量多少？
（2）现将小球拉回到竖直方向（图中B点），后由静止释放，小球通过A点位置时的
速度大小是多少？

Answer 1

分析：（1）对小球受力分析，受到重力、电场力和细线的拉力，根据电场力方向与场强方向的关系判断电性，根据共点力平衡条件和电场力F=qE列式求解电量．
（2）根据动能定理求解小球通过A点位置时的速度大小．

解答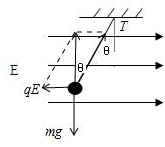：解：（1）对小球受力分析：重力、电场力和细线的拉力，如图，因电场力方向与场强方向相反，所以小球带负电．
图中θ=30°，由平衡条件得：mgtanθ=qE
解得，q=

mgtanθ

E

=

3 mg

3E

．
（2）小球从最低点到A的过程，根据动能定理得：
-mgL（1-cos30°）+qELsin30°=

1

2

m

v

2 A

解得，v_A=

2( 2 3 3 -1)gh

．
答：（1）小球带负电，电量为

3 mg

3E

．
（2）现将小球拉回到竖直方向（图中B点），后由静止释放，小球通过A点位置时的速度大小是

2( 2 3 3 -1)gh

．

点评：本题关键是对小球受力分析，然后根据共点力平衡条件并通过合成法求解．运用动能定理时，电场力做功应为qEd，d是沿电场线方向的距离．