题目内容
 回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.
回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.(1)当今医学成像诊断设备PET/CT堪称“现代医学高科技之冠”,它在医疗诊断中,常利用能放射电子的同位素碳11为示踪原子,碳11是由小型回旋加速器输出的高速质子轰击氮14获得,同时还产生另一粒子,试写出核反应方程.若碳11的半衰期τ为20min,经2.0h剩余碳11的质量占原来的百分之几?(结果取2位有效数字)
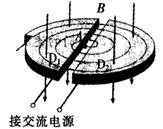
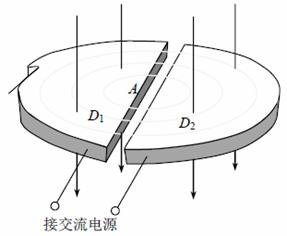
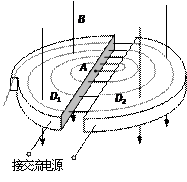
(2)回旋加速器的原理如图,D1和D2是两个中空的半径为R的半圆金属盒,它们接在电压一定、频率为f的交流电源上,位于D1圆心处的质子源A能不断产生质子(初速度可以忽略,重力不计),它们在两盒之间被电场加速,D1、D2置于与盒面垂直的磁感应强度为B的匀强磁场中.若质子束从回旋加速器输出时的平均功率为P,求输出时质子束的等效电流I与P、B、R、f的关系式(忽略质子在电场中运动的时间,其最大速度远小于光速)
(3)试推理说明:质子在回旋加速器中运动时,随轨道半径r的增大,同一盒中相邻轨道的半径之差△r是增大、减小还是不变?
分析:(1)根据质量数守恒和核电荷数守恒书写核反应方程式.根据半衰期的定义写成剩余质量和总质量的关系式即可求解.
(2)根据电流的定义式I=
和Q=Nq以及P=
求解.
(3)求出rk所对应的加速次数和rk+1所对应的加速次数即可求出它们所对应的轨道半径,然后作差即可求出rk和rk+1,从而求出△rk,运用同样的方法求出△rk+1,比较△rk和△rk+1即可得出答案.
(2)根据电流的定义式I=
| Q |
| t |
N
| ||
| t |
(3)求出rk所对应的加速次数和rk+1所对应的加速次数即可求出它们所对应的轨道半径,然后作差即可求出rk和rk+1,从而求出△rk,运用同样的方法求出△rk+1,比较△rk和△rk+1即可得出答案.
解答:解:(1)核反应方程为714N+11H→611C+24He…①
设碳11原有质量为m0,经过t=2.0h剩余的质量为mt,根据半衰期定义,有:
=(
)
=(
)
=1.6%…②
(2)设质子质量为m,电荷量为q,质子离开加速器时速度大小为v,由牛顿第二定律知:qvB=m
…③
质子运动的回旋周期为:T=
=
…④
由回旋加速器工作原理可知,交变电源的频率与质子回旋频率相同,由周期T与频率f的关系可得:f=
…⑤
设在t时间内离开加速器的质子数为N,则质子束从回旋加速器输出时的平均功率P=
…⑥
输出时质子束的等效电流为:I=
…⑦
由上述各式得I=
(3)方法一:
设k(k∈N*)为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),△rk=rk+1-rk,
在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U,
由动能定理知2qU=
m
-
m
…⑧
由洛伦兹力充当质子做圆周运动的向心力,知rk=
,
则2qU=
(
-
)…⑨
整理得 △rk=
…⑩
因U、q、m、B均为定值,令C=
,由上式得△rk=
…(11)
相邻轨道半径rk+1,rk+2之差△rk+1=rk+2-rk+1
同理 △rk=
因为rk+2>rk,比较△rk,△rk+1得△rk+1<△rk
说明随轨道半径r的增大,同一盒中相邻轨道的半径之差△r减小
方法二:
设k(k∈N*)为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),△rk=rk+1-rk,
在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U
由洛伦兹力充当质子做圆周运动的向心力,知rk=
,故
=
…(12)
由动能定理知,质子每加速一次,其动能增量△Ek=qU …(13)
以质子在D2盒中运动为例,第k次进入D2时,被电场加速(2k-1)次
速度大小为vk=
…(14)
同理,质子第(k+1)次进入D2时,被电场加速(2k+1)次,速度大小为vk+1=
综合上述各式可得
=
=
整理得
=
,
=
△rk=
同理,对于相邻轨道半径rk+1,rk+2,△rk+1=rk+2-rk+1,整理后有
△rk+1=
由于rk+2>rk,比较△rk,△rk+1得△rk+1<△rk
说明随轨道半径r的增大,同一盒中相邻轨道的半径之差△r减小,用同样的方法也可得到质子在D1盒中运动时具有相同的结论.
设碳11原有质量为m0,经过t=2.0h剩余的质量为mt,根据半衰期定义,有:
| mt |
| m0 |
| 1 |
| 2 |
| t |
| τ |
| 1 |
| 2 |
| 120 |
| 20 |
(2)设质子质量为m,电荷量为q,质子离开加速器时速度大小为v,由牛顿第二定律知:qvB=m
| v2 |
| R |
质子运动的回旋周期为:T=
| 2πR |
| v |
| 2πm |
| qB |
由回旋加速器工作原理可知,交变电源的频率与质子回旋频率相同,由周期T与频率f的关系可得:f=
| 1 |
| T |
设在t时间内离开加速器的质子数为N,则质子束从回旋加速器输出时的平均功率P=
N?
| ||
| t |
输出时质子束的等效电流为:I=
| Nq |
| t |
由上述各式得I=
| P |
| πBR2f |
(3)方法一:
设k(k∈N*)为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),△rk=rk+1-rk,
在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U,
由动能定理知2qU=
| 1 |
| 2 |
| v | 2 k+1 |
| 1 |
| 2 |
| v | 2 k |
由洛伦兹力充当质子做圆周运动的向心力,知rk=
| mvk |
| qB |
则2qU=
| q2B2 |
| 2m |
| r | 2 k+1 |
| r | 2 k |
整理得 △rk=
| 4mU |
| qB2(rk+1-rk) |
因U、q、m、B均为定值,令C=
| 4mU |
| qB2 |
| C |
| rk+rk+1 |
相邻轨道半径rk+1,rk+2之差△rk+1=rk+2-rk+1
同理 △rk=
| C |
| rk+1+rk+2 |
因为rk+2>rk,比较△rk,△rk+1得△rk+1<△rk
说明随轨道半径r的增大,同一盒中相邻轨道的半径之差△r减小
方法二:
设k(k∈N*)为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),△rk=rk+1-rk,
在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U
由洛伦兹力充当质子做圆周运动的向心力,知rk=
| mvk |
| qB |
| rk |
| rk+1 |
| vk |
| vk+1 |
由动能定理知,质子每加速一次,其动能增量△Ek=qU …(13)
以质子在D2盒中运动为例,第k次进入D2时,被电场加速(2k-1)次
速度大小为vk=
|
同理,质子第(k+1)次进入D2时,被电场加速(2k+1)次,速度大小为vk+1=
|
综合上述各式可得
| rk |
| rk+1 |
| vk |
| vk+1 |
|
整理得
| ||
|
| 2k-1 |
| 2k+1 |
| ||||
|
| 2 |
| 2k+1 |
△rk=
2
| ||
| (2k+1)(rk+rk+1) |
同理,对于相邻轨道半径rk+1,rk+2,△rk+1=rk+2-rk+1,整理后有
△rk+1=
2
| ||
| (2k+1)(rk+1+rk+2) |
由于rk+2>rk,比较△rk,△rk+1得△rk+1<△rk
说明随轨道半径r的增大,同一盒中相邻轨道的半径之差△r减小,用同样的方法也可得到质子在D1盒中运动时具有相同的结论.
点评:本题的难点是(3),要求△rk需要知道rk和rk+1,同理算出△rk+1,对△rk和△rk+1,即可得出答案.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 为
为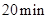 ,经
,经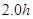 剩余碳11的质量占原来的百分之几?(结果取两位有效数字)
剩余碳11的质量占原来的百分之几?(结果取两位有效数字)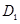 和
和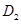 是两个1中空半经为R的半圆金属盒,它们接在电压一定、频率为
是两个1中空半经为R的半圆金属盒,它们接在电压一定、频率为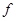 的交流电源上,位于
的交流电源上,位于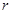 的增大,同一盒中相邻轨道的半径之差
的增大,同一盒中相邻轨道的半径之差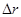 是增大、减小还是不变?
是增大、减小还是不变?