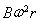题目内容
 如图所示,圆盘绕轴匀速转动时,在距离圆心0.8m处放一质量为0.4kg的金属块,恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度为2rad/s.求:
如图所示,圆盘绕轴匀速转动时,在距离圆心0.8m处放一质量为0.4kg的金属块,恰好能随圆盘做匀速圆周运动而不被甩出,此时圆盘的角速度为2rad/s.求:(1)金属块的线速度和金属块的向心加速度.
(2)金属块受到的最大静摩擦力.
(3)若把金属块放在距圆心1.25m处,在角速度不变的情况下,金属块还能随圆盘做匀速圆周运动吗?并说明理由.
分析:(1)由半径和角速度根据公式v=ωR求出线速度,由a=ω2R,求出向心加速度.
(2)金属块随圆盘恰好能做匀速圆周运动,由最大静摩擦力提供向心力,由牛顿第二定律求解最大静摩擦力.
(3)因为角速度不变,金属块距圆心的距离越大,根据F合=mω2可知,金属块随圆盘做圆周运动需要的向心力越大,而圆盘对金属块的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人金属块能随圆盘做匀速圆周运动.
(2)金属块随圆盘恰好能做匀速圆周运动,由最大静摩擦力提供向心力,由牛顿第二定律求解最大静摩擦力.
(3)因为角速度不变,金属块距圆心的距离越大,根据F合=mω2可知,金属块随圆盘做圆周运动需要的向心力越大,而圆盘对金属块的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以人金属块能随圆盘做匀速圆周运动.
解答:解:(1)根据线速度与角速度的关系得:
v=ωr=1.6m/s
根据a=ω2r
解得a=3.2m/s2
(2)金属块随圆盘恰好能做匀速圆周运动,由最大静摩擦力提供向心力,则有:
解得:
(3)因为角速度不变,金属块距圆心的距离越大,根据F合=mω2可知,金属块随圆盘做圆周运动需要的向心力越大,而圆盘对金属块的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以金属块能随圆盘做匀速圆周运动.
答:(1)金属块的线速度为1.6m/s,金属块的向心加速度为3.2m/s2.
(2)金属块受到的最大静摩擦力为1.28N.
(3)在角速度不变的情况下,金属块不能随圆盘做匀速圆周运动.
v=ωr=1.6m/s
根据a=ω2r
解得a=3.2m/s2
(2)金属块随圆盘恰好能做匀速圆周运动,由最大静摩擦力提供向心力,则有:
解得:
|
(3)因为角速度不变,金属块距圆心的距离越大,根据F合=mω2可知,金属块随圆盘做圆周运动需要的向心力越大,而圆盘对金属块的最大静摩擦力不变,提供的静摩擦力小于需要的向心力,所以金属块能随圆盘做匀速圆周运动.
答:(1)金属块的线速度为1.6m/s,金属块的向心加速度为3.2m/s2.
(2)金属块受到的最大静摩擦力为1.28N.
(3)在角速度不变的情况下,金属块不能随圆盘做匀速圆周运动.
点评:本题应用牛顿第二定律处理圆周运动的临界问题,关键分析临界条件:当物体刚要滑动时,静摩擦力达到最大值.

练习册系列答案
相关题目
 (2008?东莞模拟)如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是( )
(2008?东莞模拟)如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是( ) 如图所示,电阻不计的金属圆盘,半径为r,在圆盘边缘的槽内绕有一根很长的轻质绳,绳端吊有一质量为m的物体,圆盘处于磁感强度为B.方向垂直盘面的匀强磁场中,在圆盘中心转轴O与边缘之间接有一个电阻R.现将物体由静止释放,则圆盘绕轴O转动的最大角速度是多少?(不计一切摩擦)
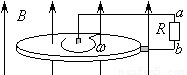
如图所示,电阻不计的金属圆盘,半径为r,在圆盘边缘的槽内绕有一根很长的轻质绳,绳端吊有一质量为m的物体,圆盘处于磁感强度为B.方向垂直盘面的匀强磁场中,在圆盘中心转轴O与边缘之间接有一个电阻R.现将物体由静止释放,则圆盘绕轴O转动的最大角速度是多少?(不计一切摩擦)