题目内容
11.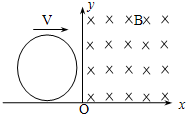 如图所示,一根电阻为R=0.6Ω的导线弯成一个圆形线圈,圆半径r=1m,圆形线圈质量m=1kg,此线圈放在绝缘光滑的水平面上,在y轴右侧有垂直于线圈平面B=0.5T的匀强磁场.若线圈以初动能Ek0=5J沿x轴方向滑进磁场,当进入磁场0.5m时,线圈中产生的电热为Q=3J.求:
如图所示,一根电阻为R=0.6Ω的导线弯成一个圆形线圈,圆半径r=1m,圆形线圈质量m=1kg,此线圈放在绝缘光滑的水平面上,在y轴右侧有垂直于线圈平面B=0.5T的匀强磁场.若线圈以初动能Ek0=5J沿x轴方向滑进磁场,当进入磁场0.5m时,线圈中产生的电热为Q=3J.求:(1)此时线圈的运动速度;
(2)此时线圈与磁场左边缘两交接点间的电压;
(3)此时线圈加速度大小.
分析 (1)由能量守恒定律可以求出线圈运动速度;
(2)由E=BLv求出感应电动势,由欧姆定律可以求出电压;
(3)由安培力公式和牛顿第二定律结合可以求出加速度.
解答 解:(1)由能量守恒定律得:
Ek0=E+$\frac{1}{2}$mv2,
代入数据解得:v=$\sqrt{\frac{2({E}_{k0}-E)}{m}}$=$\sqrt{\frac{2×(5-3)}{1}}$=2m/s;
(2)进入磁场x=0.5m时,切割磁感线的有效长度:
L=2$\sqrt{{r}^{2}-(r-x)^{2}}$=2×$\sqrt{{1}^{2}-(1-0.5)^{2}}$=$\sqrt{3}$m
圆弧所对应的圆心角为:θ=120°
感应电动势:E=BLv=0.5×$\sqrt{3}$×2=$\sqrt{3}$V
线圈在磁场外的电阻为:R′=R-$\frac{R}{360°}$×120°=$\frac{2}{3}$R
线圈与磁场左边缘两交接点间的电压:
U=IR′=$\frac{E}{R}$•$\frac{2}{3}$R=$\frac{2\sqrt{3}}{3}$V;
(3)线圈受到的安培力:F=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$
由牛顿第二定律得:F=ma
代入数据解得:a=2.5m/s2.
答:
(1)此时线圈的运动速度2m/s;
(2)此时线圈与磁场左边缘两交接点间的电压为$\frac{{2\sqrt{3}}}{3}V$;
(3)此时线圈加速度a的大小2.5m/s2
点评 本题考查了求电能、电压、加速度,应用能量守恒定律、E=BLv、欧姆定律、牛顿第二定律即可正确解题;线圈与磁场左边缘两交接点间的电压是外电压,不是感应电动势.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
19.关于运动的性质,以下说法中正确的是( )
| A. | 曲线运动一定是变速运动 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 曲线运动的加速度可以不变 | |
| D. | 物体加速度、速度大小都不变的运动一定是直线运动 |
6.下列说法中正确的是( )
| A. | 知道水蒸气的摩尔体积和水分子的体积,可计算出阿伏加德罗常数 | |
| B. | 硬币或钢针能浮于水面上,是由于液体表面张力的作用 | |
| C. | 墨水滴入水中出现扩散现象,这是分子无规则运动的结果 | |
| D. | 当分子间距离减小时,分子间斥力增大,引力减小 |
16.质量为m的汽车以恒定功率P启动后沿水平道路行驶,经过一段时间后将达到最大速度v.若行驶中受到的摩擦阻力大小不变,则在加速过程中车速为$\frac{1}{3}$v时,汽车的加速度大小为( )
| A. | $\frac{3P}{mv}$ | B. | $\frac{2P}{mv}$ | C. | $\frac{P}{mv}$ | D. | $\frac{4P}{mv}$ |
20.关于万有引力定律,以下说法正确的是( )
| A. | 两个质点之间万有引力的大小与它们质量的乘积成正比、与它们之间距离的二次方成反比 | |
| B. | 两个质点之间万有引力的大小与引力常量G成正比 | |
| C. | 万有引力定律对质量大的物体适用,对质量小的物体不适用 | |
| D. | 两物体间的万有引力符合牛顿第三定律 |
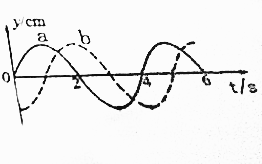 一列简谐横波在波沿直线传播,已知介质中a,b两质点平衡位置间的距离为S=3.5m,且有λ<S<2λ,a,b两点的振动情况分别如图中实线和虚线所示,求:
一列简谐横波在波沿直线传播,已知介质中a,b两质点平衡位置间的距离为S=3.5m,且有λ<S<2λ,a,b两点的振动情况分别如图中实线和虚线所示,求: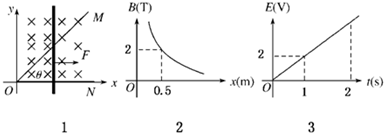
 石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖.用石墨烯制作超级缆绳,人类搭建“太空电梯”的梦想有望在本世纪实现.科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换.(地面附近重力加速度g取10m/s2,地球自转角速度ω=7.2×10-5rad/s,地球半径R=6.4×103km.计算结果保留3位有效数字)
石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖.用石墨烯制作超级缆绳,人类搭建“太空电梯”的梦想有望在本世纪实现.科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换.(地面附近重力加速度g取10m/s2,地球自转角速度ω=7.2×10-5rad/s,地球半径R=6.4×103km.计算结果保留3位有效数字)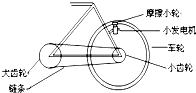 如图所示是自行车传动装置的示意图.请思考并回答:假设脚踏板转动周期为T,为了测出自行车前进的速度,需要测出的物理量有:大齿轮(主动齿轮或轮盘)半径R1、小齿轮(被动齿轮或飞轮)半径R2、后轮半径R3,若用所测得的字母来表示自行车的前进速度,则其表达式为V=$\frac{2π{R}_{1}{R}_{3}}{T{R}_{2}}$.
如图所示是自行车传动装置的示意图.请思考并回答:假设脚踏板转动周期为T,为了测出自行车前进的速度,需要测出的物理量有:大齿轮(主动齿轮或轮盘)半径R1、小齿轮(被动齿轮或飞轮)半径R2、后轮半径R3,若用所测得的字母来表示自行车的前进速度,则其表达式为V=$\frac{2π{R}_{1}{R}_{3}}{T{R}_{2}}$.