题目内容
9.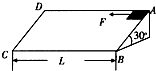 质量为m的小物块静置于倾角为30°,边长为L的正方形斜面上的A点,如图所示,小物块与斜面间的动摩擦因数为$\frac{\sqrt{2}}{2}$,某时刻给小物块施加一个沿与BC方向平行,大小为$\frac{1}{2}$mg的恒定外力F,小物块运动到BC边时的速度为v.下列对小物块描述正确的有( )
质量为m的小物块静置于倾角为30°,边长为L的正方形斜面上的A点,如图所示,小物块与斜面间的动摩擦因数为$\frac{\sqrt{2}}{2}$,某时刻给小物块施加一个沿与BC方向平行,大小为$\frac{1}{2}$mg的恒定外力F,小物块运动到BC边时的速度为v.下列对小物块描述正确的有( )| A. | 小物块到达BC边时,所受重力的瞬时功率为$\frac{1}{2}$mgv | |
| B. | 此过程中,小物块所受恒定外力F的平均功率为$\frac{\sqrt{2}}{8}$mgv | |
| C. | 此过程中.小物块机械能的改变量为$\frac{1-\sqrt{3}}{2}$mgL | |
| D. | 此过程中.所产生的焦耳热为$\frac{\sqrt{3}}{2}$mgL |
分析 先对物块进行受力分析,判断出物块做匀加速直线运动,根据瞬时功率的定义式求出重力的功率和拉力F 的功率;根据功能关系求出产生的焦耳热.
解答 解:对物块进行受力分析可知,它受到重力.斜面的支持力和摩擦力、以及拉力F的作用,在垂直于斜面的方向,支持力:${F}_{N}=mgcos30°=\frac{\sqrt{3}}{2}mg$
所以物块受到的摩擦力:f=μFN=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}mg=\frac{\sqrt{6}}{4}mg$
重力沿斜面方向的分力:${G}_{1}=mgsin30°=\frac{1}{2}mg$
物块在沿斜面的平面内的受力如图,则:
由图可知,合力的方向与BC之间的夹角θ:$tanθ=\frac{{G}_{1}}{F}=\frac{\frac{1}{2}mg}{\frac{1}{2}mg}=1$,则θ=45°
小物块运动到BC边时的速度为v,所以沿F方向的分受到:${v}_{F}=v•cos45°=\frac{\sqrt{2}}{2}v$
沿斜面向下的分速度:${v}_{{G}_{1}}=v•sin45°=\frac{\sqrt{2}}{2}v$
沿斜面向下的分速度在竖直向下的方向上的分速度:${v}_{下}={v}_{G1}•sin30°=\frac{\sqrt{2}}{4}v$
A、小物块到达BC边时,所受重力的瞬时功率为${P}_{G}=mg•{v}_{下}=mg×\frac{\sqrt{2}}{4}v$.故A错误;
B、此过程中,小物块所受恒定外力F的平均功率为${P}_{F}=F•{v}_{F}=\frac{1}{2}mg•\frac{\sqrt{2}}{2}v=\frac{\sqrt{2}}{4}mgv$.故B错误;
C、此过程中,拉力做的功:${W}_{1}=F•L=\frac{1}{2}mgL$,克服摩擦力做的功:${W}_{2}=f•\sqrt{2}L=\frac{\sqrt{6}}{4}mg•\sqrt{2}L=\frac{\sqrt{3}}{2}mgL$,所以机械能的该变量:
△E=W1-W2=$\frac{1-\sqrt{3}}{2}$mgL.故C正确.
D、此过程中.克服摩擦力做的功是$\frac{\sqrt{3}}{2}$mgL,所以产生的焦耳热为$\frac{\sqrt{3}}{2}$mgL.故D正确.
故选:CD
点评 本题物体受力分布在立体空间,解答的关键是将力分成垂直于斜面和平行于斜面两平面内研究,垂直于斜面的平面内物体的合力为零.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | 电磁打点计时器使用的是220V交流电源 | |
| B. | 实验时应该先通电,后让纸带运动 | |
| C. | 计时器打点时间间隔与电源电压有关 | |
| D. | 利用纸带上的点能精确的求出打某点时纸带的瞬时速度 | |
| E. | 当纸带运动速度增大时,两点的间距增大 |

| A. | 图乙将停于P点前面某处 | B. | 图丙将停于P点前面某处 | ||
| C. | 图乙将停于P点后面某处 | D. | 图丙将停于P点处 |
| A. | 根据定义式B=$\frac{F}{IL}$,磁场中某点的磁感强度B与F成正比,与IL成反比 | |
| B. | 磁感强度B是矢量,方向与安培力F的方向相同 | |
| C. | 磁感强度B是矢量,方向与通过该点的磁感线的切线方向相同 | |
| D. | 在确定的磁场中,同一点的磁感应强度是确定的,不同点的磁感应强度可能不同,磁感线密的地方磁感应强度大些,磁感线疏的地方磁感应强度小些 |
| A. | 只要有光照射到金属表面就会有电子从表面逸出 | |
| B. | 只有光的强度大于某个值时才会发生光电效应现象 | |
| C. | 只有光的波长大于某个值时才会发生光电效应现象 | |
| D. | 只有光的频率大于某个值时才会发生光电效应现象 |
| A. | 并联用电器增多,电路的总电阻增大 | |
| B. | 并联用电器增多,电路的总电流减小 | |
| C. | 并联用电器增多,家用电器的实际功率减小 | |
| D. | 并联用电器增多,家用电器的额定功率减小 |
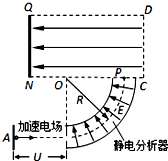 如图,静止于A处的离子,经加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐射分布的电场,已知圆弧虚线的半径为R,其所在处场强为E、方向如图所示;离子质量为m、电荷量为q;$\overline{ON}$=2d、$\overline{PN}$=3d,离子重力不计.
如图,静止于A处的离子,经加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐射分布的电场,已知圆弧虚线的半径为R,其所在处场强为E、方向如图所示;离子质量为m、电荷量为q;$\overline{ON}$=2d、$\overline{PN}$=3d,离子重力不计.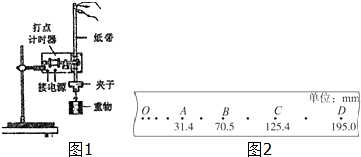 (1)下面列举了该实验的几个操作步骤:
(1)下面列举了该实验的几个操作步骤: