题目内容
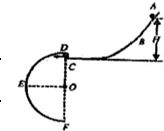
如图所示，A BC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合．现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，g取10m/s2．以下说法正确的是（ ）
A．若使小球经C处水平进入轨道DEF且能沿轨道运动，H至少为0.4m
B．若使小球经C处水平进入轨道DEF且能沿轨道运动，H至少为0.2m
C．若H小于0.2m，则小球不可能沿DEF轨道运动
D．若H小于0.2m，则小球不可能到达E点
【答案】分析：小球从ABC轨道下滑，机械能守恒，设到达C点时的速度大小为υ．小球能在竖直平面内做圆周运动，在圆周最高点必须满足mg≤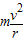
，联立即可求解H；
若h＜H，小球过C点后做平抛运动，设球经C点时的速度大小为υx，根据自由落体运动的规律结合机械能守恒即可判断能否到达E点．
解答：解：A、B、C、小球从ABC轨道下滑，机械能守恒，设到达C点时的速度大小为υ．则：mgH=
mv2…①
小球能在竖直平面内做圆周运动，在圆周最高点必须满足：mg≤m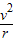
…②
①、②联立并代入数据得：H≥0.2m
故A错误，B正确，C正确；
D、若h＜0.2m，小球过C点后与轨道分离而做平抛运动，设球经C点时的速度大小为υx，则击中E点时：
竖直方向：r=
gt2…③
水平方向：r=υxt…④
由机械能守恒有：mgh=
mυx2…⑤
联立③、④、⑤并代入数据得h=0.1m
故D错误；
故选BC．
点评：本题是圆周运动结合平抛运动的题型，要知道小球能在竖直平面内做圆周运动，在圆周最高点必须满足mg≤m
，若不满足，则小球做平抛运动，难度适中．
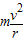，联立即可求解H；若h＜H，小球过C点后做平抛运动，设球经C点时的速度大小为υx，根据自由落体运动的规律结合机械能守恒即可判断能否到达E点．
解答：解：A、B、C、小球从ABC轨道下滑，机械能守恒，设到达C点时的速度大小为υ．则：mgH=
mv2…①小球能在竖直平面内做圆周运动，在圆周最高点必须满足：mg≤m
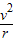…②①、②联立并代入数据得：H≥0.2m
故A错误，B正确，C正确；
D、若h＜0.2m，小球过C点后与轨道分离而做平抛运动，设球经C点时的速度大小为υx，则击中E点时：
竖直方向：r=
gt2…③水平方向：r=υxt…④
由机械能守恒有：mgh=
mυx2…⑤联立③、④、⑤并代入数据得h=0.1m
故D错误；
故选BC．
点评：本题是圆周运动结合平抛运动的题型，要知道小球能在竖直平面内做圆周运动，在圆周最高点必须满足mg≤m
，若不满足，则小球做平抛运动，难度适中． 
练习册系列答案
阅读快车系列答案
相关题目
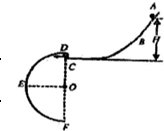如图所示，A BC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合．现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，g取10m/s2．以下说法正确的是（ ）
（2008?黄冈一模）如图所示，斜面AB和水平面BC是由相同绝缘材料组成的静止开始释放，它运动到C点时的速度为v1（v1≠0），最终停下的位置到A点的水平位移为s1；若让该小滑块带上正电荷，并在整个空间施加竖直向下的匀强电场，仍让小滑块从A处由静止开始释放，它运动到C点时的速度为v2，最终停下时到A点的水平位移为s2，设斜面与水平面连接处是圆滑的，且水平面足够长，则以下判断正确的是（ ）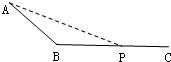
如图所示，斜面AB和水平面BC是由同一板材上截下的两段，在B处用小圆弧连接．将小铁块（可视为质点）从A处由静止释放后，它沿斜面向下滑行，进入平面，最终静止于P处．若从该板材上再截下一段，搁置在A、P之间，构成一个新的斜面，再将铁块放回A处，并轻推一下使之沿新斜面向下滑动．关于此情况下铁块运动情况的描述，正确的是（ ）