题目内容
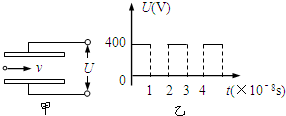 (2008?普陀区三模)两平行金属板长L=0.1m,板间距离d=1.44×10-2m,从两板左端正中间有带电粒子持续飞入,如图甲所示.粒子的电量q=10-10C,质量m=10-20kg,初速度方向平行于极板,大小为v=107m/s,在两极板上加一按如图乙所示规律变化的电压,不计带电粒子重力作用.求:
(2008?普陀区三模)两平行金属板长L=0.1m,板间距离d=1.44×10-2m,从两板左端正中间有带电粒子持续飞入,如图甲所示.粒子的电量q=10-10C,质量m=10-20kg,初速度方向平行于极板,大小为v=107m/s,在两极板上加一按如图乙所示规律变化的电压,不计带电粒子重力作用.求:(1)带电粒子如果能从金属板右侧飞出,粒子在电场中运动的时间是多少?
(2)有一粒子恰好能从右侧极板边缘飞出,该粒子飞出时动能的增量△Ek=?
(3)该装置正常工作后,在一个周期内从两板右侧有粒子射出的时间t与无粒子射出的时间t?各为多少?(打到金属板上的粒子立即被金属板吸附)
分析:(1)金属板间有电场时,带电粒子做类平抛运动,无电场时,做匀速直线运动,水平方向总是做匀速直线运动,由t=
求时间;
(2)带电粒子在极板间运动期间,在竖直方向有一段时间加速,有一段时间匀速,分两种情况:先匀速再加速和先加速再匀速,由牛顿第二定律求出加速度,由运动学公式求出偏移距离,再由动能定理求粒子飞出时动能的增量△Ek.
(3)根据(2)问的结果分析粒子将打到金属板上被金属板吸附的时间段.在(1~2)×10-8s内某时刻t2前进入极板的粒子沿竖直方向先不偏转后加速,直至通过极板.t2时刻应满足
=
a(t2-1×10-8)2,求t2.在一个周期有粒子射出的时间为t=t2-t1.无粒子射出的时间t′=T-t.
| L |
| v |
(2)带电粒子在极板间运动期间,在竖直方向有一段时间加速,有一段时间匀速,分两种情况:先匀速再加速和先加速再匀速,由牛顿第二定律求出加速度,由运动学公式求出偏移距离,再由动能定理求粒子飞出时动能的增量△Ek.
(3)根据(2)问的结果分析粒子将打到金属板上被金属板吸附的时间段.在(1~2)×10-8s内某时刻t2前进入极板的粒子沿竖直方向先不偏转后加速,直至通过极板.t2时刻应满足
| d |
| 2 |
| 1 |
| 2 |
解答:解:(1)带电粒子在水平方向作匀速直线运动,有 t=
=
s=1×10-8s.
(2)粒子进入极板后,当两极板间有电压时,粒子的加速度大小为 a=
=
m/s2≈2.78×1014m/s2
如果进入电场的粒子在竖直方向始终加速,其偏移距离 y=
at2=
×2.78×1014×(10-8)2m=1.39×10-2m>
所以带电粒子在极板间运动期间,在竖直方向有一段时间加速,有一段时间匀速.如果先匀速再加速,从右侧极板边缘飞出的粒子动能增量为
△Ek=q×
U=2×10-8J
如果先加速再匀速,例如在(0~1)×10-8s内某时刻t1进入电场的粒子,从右侧极板边缘飞出时应满足
=
a(1×10-8-t1)2+a(1×10-8-t1)t1
解得 t1=6.9×10-9s
加速时间 t1′=(1×10-8-6.9×10-9)s=3.1×10-9s
加速距离 y=
at1′2=
×2.78×1014×(3.1×10-9)2m=1.31×10-3m
粒子动能增量为 △Ek=q
y=10-10×
×1.31×10-3J=3.6×10-9J
(3)由(2)可知,在(0~1)×10-8s内进入极板的粒子,在t1=6.9×10-9s时刻之前进入的粒子将打到金属板上被金属板吸附,在时刻t1以后进入极板的粒子沿电场方向先加速后匀速直至飞出极板;
在(1~2)×10-8s内某时刻t2前进入极板的粒子沿竖直方向先不偏转后加速,直至通过极板.t2时刻应满足
=
a(t2-1×10-8)2
可解得:t2=1.72×10-8s.
所以在一个周期有粒子射出的时间为
t=t2-t1=(1.72×10-8-6.9×10-9)s=1.03×10-8s;
无粒子射出的时间
t?=T-t=(2×10-8-1.03×10-8)s=0.97×10-8s.
答:
(1)带电粒子如果能从金属板右侧飞出,粒子在电场中运动的时间是1×10-8s.
(2)有一粒子恰好能从右侧极板边缘飞出,该粒子飞出时动能的增量为3.6×10-9J.
(3)该装置正常工作后,在一个周期内从两板右侧有粒子射出的时间为1.03×10-8s;无粒子射出的时间为0.97×10-8s.
| L |
| v |
| 0.1 |
| 107 |
(2)粒子进入极板后,当两极板间有电压时,粒子的加速度大小为 a=
| qU |
| md |
| 10-10×400 |
| 10-20×1.44×10-2 |
如果进入电场的粒子在竖直方向始终加速,其偏移距离 y=
| 1 |
| 2 |
| 1 |
| 2 |
| d |
| 2 |
所以带电粒子在极板间运动期间,在竖直方向有一段时间加速,有一段时间匀速.如果先匀速再加速,从右侧极板边缘飞出的粒子动能增量为
△Ek=q×
| 1 |
| 2 |
如果先加速再匀速,例如在(0~1)×10-8s内某时刻t1进入电场的粒子,从右侧极板边缘飞出时应满足
| d |
| 2 |
| 1 |
| 2 |
解得 t1=6.9×10-9s
加速时间 t1′=(1×10-8-6.9×10-9)s=3.1×10-9s
加速距离 y=
| 1 |
| 2 |
| 1 |
| 2 |
粒子动能增量为 △Ek=q
| U |
| d |
| 400 |
| 1.44×10-2 |
(3)由(2)可知,在(0~1)×10-8s内进入极板的粒子,在t1=6.9×10-9s时刻之前进入的粒子将打到金属板上被金属板吸附,在时刻t1以后进入极板的粒子沿电场方向先加速后匀速直至飞出极板;
在(1~2)×10-8s内某时刻t2前进入极板的粒子沿竖直方向先不偏转后加速,直至通过极板.t2时刻应满足
| d |
| 2 |
| 1 |
| 2 |
可解得:t2=1.72×10-8s.
所以在一个周期有粒子射出的时间为
t=t2-t1=(1.72×10-8-6.9×10-9)s=1.03×10-8s;
无粒子射出的时间
t?=T-t=(2×10-8-1.03×10-8)s=0.97×10-8s.
答:
(1)带电粒子如果能从金属板右侧飞出,粒子在电场中运动的时间是1×10-8s.
(2)有一粒子恰好能从右侧极板边缘飞出,该粒子飞出时动能的增量为3.6×10-9J.
(3)该装置正常工作后,在一个周期内从两板右侧有粒子射出的时间为1.03×10-8s;无粒子射出的时间为0.97×10-8s.
点评:本题粒子电子在周期性电场中,分析电子的运动情况是关键,运用运动的分解法进行研究.

练习册系列答案
相关题目
 (2008?普陀区三模)如图所示,在边长为L的正方形ABCD区域内存在着场强为E的匀强电场,电场方向与AB边平行.一带电量为q的带电粒子以mv2/2从正方形ABCD一条边的中点射入(该粒子的重力不计),一段时间后,该粒子从一条边的中点射出,此时该带电粒子的动能有n种情况,则n 等于( )
(2008?普陀区三模)如图所示,在边长为L的正方形ABCD区域内存在着场强为E的匀强电场,电场方向与AB边平行.一带电量为q的带电粒子以mv2/2从正方形ABCD一条边的中点射入(该粒子的重力不计),一段时间后,该粒子从一条边的中点射出,此时该带电粒子的动能有n种情况,则n 等于( ) (2008?普陀区三模)如图所示,OA为一质量分布均匀的横梁,横梁始终保持水平状态,被一轻质钢索AB拉着,O为无摩擦铰链,重物在水平恒力F作用下从O点出发向右作匀加速直线运动,钢索中的拉力为T,物体到O点的距离为X,物体运动的时间为t,则下图中能正确描述T-X、T-t之间关系的是( )
(2008?普陀区三模)如图所示,OA为一质量分布均匀的横梁,横梁始终保持水平状态,被一轻质钢索AB拉着,O为无摩擦铰链,重物在水平恒力F作用下从O点出发向右作匀加速直线运动,钢索中的拉力为T,物体到O点的距离为X,物体运动的时间为t,则下图中能正确描述T-X、T-t之间关系的是( ) (2008?普陀区三模)如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均由跨过滑轮的钢索系住,在电动机的牵引下电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止,在不计空气阻力和摩擦阻力的情况下,h为( )
(2008?普陀区三模)如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均由跨过滑轮的钢索系住,在电动机的牵引下电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止,在不计空气阻力和摩擦阻力的情况下,h为( )