题目内容
 (2009?南京一模)如图所示,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度v0=5m/s沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时,将一小铁块贴着挡板无初速度地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5,当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=10m/s2)试问:
(2009?南京一模)如图所示,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度v0=5m/s沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时,将一小铁块贴着挡板无初速度地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5,当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=10m/s2)试问:(1)第1个铁块放上后,木板运动了L时,木板的速度多大?
(2)最终木板上放有多少个铁块?
(3)最后一个铁块放上后,木板再向右运动的距离是多少?
分析:(1)第1个铁块放上后,木板受到向左的滑动摩擦力而做匀减速运动,由牛顿第二定律和运动学公式结合求解木板运动了L时的速度.
(2)假设最终有n个铁块能放在木板上,由牛顿第二定律求出此时的加速度,再由速度位移关系式分析第1个铁块、第2个铁块…第n个铁块放上后木板的速度,当木板的速度为0时,确定铁块的个数.
(3)由上分析得到放上n-1块铁块时木板的位移与速度,再由速度位移关系式求出后一个铁块放上后,木板再向右运动的距离.
(2)假设最终有n个铁块能放在木板上,由牛顿第二定律求出此时的加速度,再由速度位移关系式分析第1个铁块、第2个铁块…第n个铁块放上后木板的速度,当木板的速度为0时,确定铁块的个数.
(3)由上分析得到放上n-1块铁块时木板的位移与速度,再由速度位移关系式求出后一个铁块放上后,木板再向右运动的距离.
解答:解:(1)第1个铁块放上后,木板做匀减速运动,
即有:μmg=Ma1,2a1L=v02-v12
代入数据解得:v1=2
m/s.
(2)设最终有n个铁块能放在木板上,则木板运动的加速度大小为:
an=
第1个铁块放上后:2a1L=v02-v12
第2个铁块放上后:2a2L=v12-v22
…
第n个铁块放上后:2anL=
-
由上可得:(1+2+3+…+n)?2
L=v02-
木板停下时,vn=0,解得n=6.6.
即最终有7个铁块放在木板上.
(3)从放上第1个铁块至刚放上第7个铁块的过程中,由(2)中表达式可得:
?2
L=v02-v62
从放上第7个铁块至木板停止运动的过程中,设木板发生的位移是d,则:
2?
d=v62-0
解得:d=
m.
答:(1)第1个铁块放上后,木板运动了L时,木板的速度是2
m/s.
(2)最终木板上放有7个铁块.
(3)最后一个铁块放上后,木板再向右运动的距离是
m.
即有:μmg=Ma1,2a1L=v02-v12
代入数据解得:v1=2
| 6 |
(2)设最终有n个铁块能放在木板上,则木板运动的加速度大小为:
an=
| μnmg |
| M |
第1个铁块放上后:2a1L=v02-v12
第2个铁块放上后:2a2L=v12-v22
…
第n个铁块放上后:2anL=
| v | 2 n-1 |
| v | 2 n |
由上可得:(1+2+3+…+n)?2
| μmg |
| M |
| v | 2 n |
木板停下时,vn=0,解得n=6.6.
即最终有7个铁块放在木板上.
(3)从放上第1个铁块至刚放上第7个铁块的过程中,由(2)中表达式可得:
| 6×(6+1) |
| 2 |
| μmg |
| M |
从放上第7个铁块至木板停止运动的过程中,设木板发生的位移是d,则:
2?
| 7μmg |
| M |
解得:d=
| 4 |
| 7 |
答:(1)第1个铁块放上后,木板运动了L时,木板的速度是2
| 6 |
(2)最终木板上放有7个铁块.
(3)最后一个铁块放上后,木板再向右运动的距离是
| 4 |
| 7 |
点评:本题是物理上数列类型的问题,运用归纳法总结规律,得到速度的通项是关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
 (2009?南京一模)如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )
(2009?南京一模)如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( ) (2009?南京一模)用电高峰期,电灯往往会变碚,其原理可简化为如下问题如图所示,理想变压器的副线圈上,通过输电线连接两只灯泡L1和L2,输电线的等效电阻为R,原线圈输入恒定的交变电压.开始时,开关S断开,当开关S闭合时,以下说法正确的有( )
(2009?南京一模)用电高峰期,电灯往往会变碚,其原理可简化为如下问题如图所示,理想变压器的副线圈上,通过输电线连接两只灯泡L1和L2,输电线的等效电阻为R,原线圈输入恒定的交变电压.开始时,开关S断开,当开关S闭合时,以下说法正确的有( )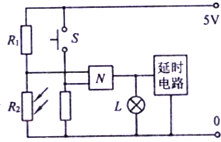 (2009?南京一模)如图所示是一个由声控开关S、光敏电阻R2、小灯泡L等元件构成的自动控制电路,该电路常用于控制居民小区里的楼道灯.白天,即使拍手发出声音,楼道灯也不会亮;到了晚上,只要拍手发出声音,灯就会亮,并采用延时电路,使之亮一段时间后才熄灭.对此电路下面说法正确的有:( )
(2009?南京一模)如图所示是一个由声控开关S、光敏电阻R2、小灯泡L等元件构成的自动控制电路,该电路常用于控制居民小区里的楼道灯.白天,即使拍手发出声音,楼道灯也不会亮;到了晚上,只要拍手发出声音,灯就会亮,并采用延时电路,使之亮一段时间后才熄灭.对此电路下面说法正确的有:( )