��Ŀ����
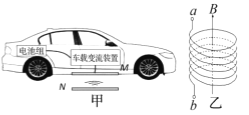
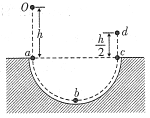
����Ŀ����ͼ��ʾ��һ�������Ӵ�ֱ������ǿ�糡�����糡ƫת��Ӵų�����߽���M����봹ֱֽ���������ǿ�ų��У����Ӵų�����߽��ϵ�N���뿪�ų�����֪�������ӵıȺ�![]() ��3.2��109 C/kg���糡ǿ��E��200 V/m��M��N���MN��1 cm�������峤L��25 cm�����ӵij��ٶ�v0��4��105 m/s�����������������Բ��ƣ���
��3.2��109 C/kg���糡ǿ��E��200 V/m��M��N���MN��1 cm�������峤L��25 cm�����ӵij��ٶ�v0��4��105 m/s�����������������Բ��ƣ���
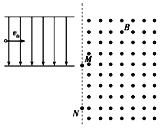
(1)��������糡ʱ���˶���������ٶ�v0�ļн�����
(2)�Ÿ�Ӧǿ��B�Ĵ�С��
���𰸡�(1)����45�㡡(2)B��2.5��10��2 T
��������
��1�������ڵ糡������ƽ���˶���Ӧ����ƽ���˶����ɿ���������ӵ�ƫת�Ƕȣ�
��2�������ڴų���������Բ���˶����������ṩ�����������������˶��켣��������ӹ���뾶��Ȼ��Ӧ��ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȣ�
��1�������ڵ糡������ƽ���˶��������ٶ�ƫ�ǵ�����ֵ��
���У���=45�㣻

��2�����ӽ���ų�ʱ���ٶȴ�СΪ��![]() ��
��
�����ڴų���������Բ���˶����������ṩ�������������˶��켣��ͼ��ʾ���ɼ���֪ʶ�ã� ��
��
��ţ�ٵڶ����ɵã�qvB=m![]() ��
��
�������ݽ�ã�B=2.5��10-2T��

��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
�����Ŀ