题目内容
(16分)、如图所示,水平绝缘光滑轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径为R。在轨道所在空间存在水平向右的匀强电场,电场强度E,现有一质量为m,带电荷量为q的带电体(可视为质点)放在水平轨道上与B端距离s =5R的位置A,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零。已知该带电体所受电场力大小为重力的 ,重力加速度为g,求:
,重力加速度为g,求:

(1)带电体在水平轨道上运动的加速度大小及运动到B端时的速度大小;
(2)带电体运动刚刚经过圆弧形轨道的B点瞬间时对圆弧轨道的压力大小;
(3)带电体沿圆弧形轨道从B到C的运动过程中,电场力和摩擦力带电体所做的功各是多少。
(1)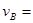
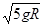 (2)N/=N=6mg(3)W=-2mgR
(2)N/=N=6mg(3)W=-2mgR
【解析】(1)在水平轨道运动时qE=ma 得a=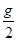 (3分)
(3分)
由动能定理 qEs=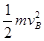 得
得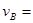
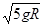 (3分)
(3分)
(2)设带电体运动到圆轨道B端时受轨道的支持力为N,根据牛顿第二定律有
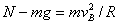 (3分) 得N=6mg
(1分)
(3分) 得N=6mg
(1分)
根据牛顿第三定律可知,带电体对圆弧轨道B端的压力大小N/=N=6mg(1分)
(3)因电场力做功与路径无关,
所以带电体沿圆弧形轨道运动过程中,电场力所做的功 W电 =qER=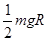 (1分)
(1分)
设带电体沿圆弧形轨道运动过程中摩擦力所做的功为W摩,对此过程根据动能定理有
qER+W-mgR=0-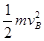 (4分)
解得 W=-2mgR (1分)
(4分)
解得 W=-2mgR (1分)
本题考查牛顿第二定律、动能定理和圆周运动规律的应用,在电场中由电场力做功等于动能的变化量可求得B点速度,在B点由支持力和重力的合力提供向心力,可求得支持力大小,由于电场力做功与路径无关只与初末位置有关,所以带电体沿圆弧形轨道运动过程中,电场力所做的功为qER,在整个过程中应用动能定理可求得克服摩擦力做功大小

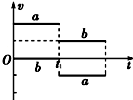
 2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示.当它们处于如图所示的轨道运行时,下列说法正确的是( )
2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示.当它们处于如图所示的轨道运行时,下列说法正确的是( )
 (1)北京时间2011年3月11日13时46分,在日本本州岛附近海域发生里氏9.0级强烈地震,地震和海啸引发福岛第一核电站放射性物质泄漏,其中放射性物质碘131的衰变方程为
(1)北京时间2011年3月11日13时46分,在日本本州岛附近海域发生里氏9.0级强烈地震,地震和海啸引发福岛第一核电站放射性物质泄漏,其中放射性物质碘131的衰变方程为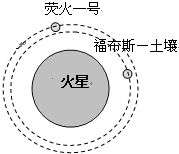 中国首颗火星探测器“萤火一号”同俄罗斯“福布斯-土壤”探测器于北京时间2011年11月9日4时16分在位于哈萨克斯坦境内的拜科努尔发射场搭乘俄运载火箭发射升空.如果“萤火一号”和“福布斯-土壤”两颗探测器能够顺利进入预定轨道(如图所示),人类将首次实现利用处于不同位置的两个航天器来同时对火星电离层和磁场进行研究.下列说法正确的是( )
中国首颗火星探测器“萤火一号”同俄罗斯“福布斯-土壤”探测器于北京时间2011年11月9日4时16分在位于哈萨克斯坦境内的拜科努尔发射场搭乘俄运载火箭发射升空.如果“萤火一号”和“福布斯-土壤”两颗探测器能够顺利进入预定轨道(如图所示),人类将首次实现利用处于不同位置的两个航天器来同时对火星电离层和磁场进行研究.下列说法正确的是( )