题目内容
20.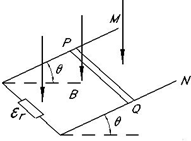 如图所示,两条间距为d,表面光滑的平行金属导轨M、N,导轨平面与水平面的倾角为θ,导轨的一端有一电池组与M、N相连,整个装置处在方向竖直向下、磁感强度为B的匀强磁场中.现将一质量为m的水平金属棒PQ与轨道垂直地置于导轨上,这时两导轨与金属棒在回路中的电阻值为R,PQ棒刚好处于静止状态.设电池组的内阻为r,试计算电池组的电动势E,并标明极性.
如图所示,两条间距为d,表面光滑的平行金属导轨M、N,导轨平面与水平面的倾角为θ,导轨的一端有一电池组与M、N相连,整个装置处在方向竖直向下、磁感强度为B的匀强磁场中.现将一质量为m的水平金属棒PQ与轨道垂直地置于导轨上,这时两导轨与金属棒在回路中的电阻值为R,PQ棒刚好处于静止状态.设电池组的内阻为r,试计算电池组的电动势E,并标明极性.
分析 根据左手定则,结合受力分析,及力的分解法则与平衡条件,根据安培力大小公式,与闭合电路欧姆定律,即可求解
解答 解:如图,金属棒受mg、N和F作用处于静止,依平衡条件,可知F方向必水平向右,再依左手定则可知金属棒电流流向是P流向Q;故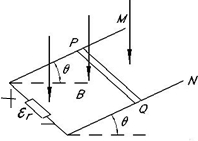
对金属棒依平衡条件得:Nsinθ=F
Ncosθ=mg
根据安培力大小公式F=BIL
及闭合电路欧姆定律,E=I(r+R)
由上两式,解得:$E=\frac{mg(R+r)tanθ}{BL}$
答:电池组的电动势E为$\frac{mg(R+r)tanθ}{BL}$,正负极如图所示
点评 考查左手定则与力的平行四边形定则的应用,掌握安培力表达式成立条件,理解闭合电路欧姆定律的内容

练习册系列答案
相关题目
8.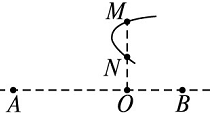 如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上三点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,则下列判断不正确的是( )
如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上三点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,则下列判断不正确的是( )
 如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上三点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,则下列判断不正确的是( )
如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上三点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别为EM、EN,电势分别为φM、φN,则下列判断不正确的是( )| A. | A点电荷一定带正电 | |
| B. | 试探电荷在M处的电势能小于在N处的电势能 | |
| C. | EM一定小于EN,φM可能小于φN | |
| D. | UMN=UNO |
5.关于摩擦力与弹力的关系,下列说法中正确的是( )
| A. | 有弹力一定有摩擦力 | |
| B. | 有弹力不一定有摩擦力? | |
| C. | 有摩擦力一定有弹力? | |
| D. | 同一接触面上的弹力和摩擦力的方向一定平行 |
12.单位电荷绕闭合电路一周,如外电路是纯电阻电路,外电路中产生的热量仅决定于( )
| A. | 电流的大小,且与电流的平方成正比 | |
| B. | 电源电动势的大小,且与电动势的大小成正比 | |
| C. | 路端电压的大小,且与路端电压的大小成正比 | |
| D. | 各部分电阻值的大小,且与电阻值成反比 |
9.下面的说法正确的是( )
| A. | 1638年,伽利略用科学推理论证重物体和轻物体下落一样快;并在比萨斜塔做了两个不同质量的小球下落的实验,证明了他的观点是正确的 | |
| B. | 静止的火车启动时速度变化慢,是因为物体静止时惯性大 | |
| C. | 伽利略通过理想斜面实验推出力不是维持物体运动的原因 | |
| D. | 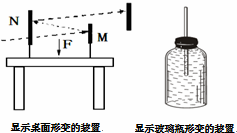 如图两个实验,共同用到的是放大的思想方法 |

 长为L的轻杆两端各连接一个质量均为m的小球,以它们的中心为轴,在竖直面内做匀速圆周运动,转动周期为T=2π$\sqrt{\frac{L}{g}}$,求它们通过竖直位置时,上下两球分别对杆端的作用力?并说明是拉力还是压力?
长为L的轻杆两端各连接一个质量均为m的小球,以它们的中心为轴,在竖直面内做匀速圆周运动,转动周期为T=2π$\sqrt{\frac{L}{g}}$,求它们通过竖直位置时,上下两球分别对杆端的作用力?并说明是拉力还是压力?