题目内容
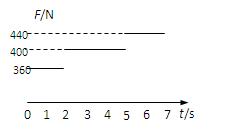
一质量m=40kg的小孩站在竖直电梯内的体重计上．电梯从t=0时刻由静止开始启动，在0到7s内体重计示数F的变化如图所示．试问：
（1）小孩乘电梯是上楼还是下楼？简述理由；
（2）在这段时间内电梯运动的距离是多少？取g=10m/s2．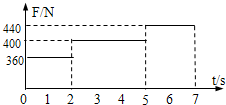
（1）小孩乘电梯是上楼还是下楼？简述理由；
（2）在这段时间内电梯运动的距离是多少？取g=10m/s2．
（1）由图可知，开始的2s时间内体重计的示数F=360N小于其重力（mg=400N），即处于失重状态，说明电梯是竖直向下加速的．所以是下楼．
（2）由牛顿第二定律得：0～2s时间内有 mg-F1=ma1
代入数据解之得 a1=1m/s2
由公式x=
at2得，
电梯加速位移为：x1=
a1
=2m
由公式v=at得：
开始匀速运动的速度为：v1=a1
=2m/s
2s～5s时间内因F2=mg，所以电梯以v1做匀速直线运动，
位移为：x2=v1t2=6m
5s～7s时间内因F3＞mg，所以电梯做向下的匀减速运动，
由牛顿第二定律得：F3-mg=ma3
代入数据解之得 a3=1m/s2
由公式x=v0t+
at2得；
减速运动的位移为：x3=v1t3-
a3
=2m
这段时间内电梯下降的距离X=x1+x2+x3=10m
答：（1）下楼
（2）在这段时间内电梯运动的距离是10m．
（2）由牛顿第二定律得：0～2s时间内有 mg-F1=ma1
代入数据解之得 a1=1m/s2
由公式x=
| 1 |
| 2 |
电梯加速位移为：x1=
| 1 |
| 2 |
| t | 21 |
由公式v=at得：
开始匀速运动的速度为：v1=a1
| t | 1 |
2s～5s时间内因F2=mg，所以电梯以v1做匀速直线运动，
位移为：x2=v1t2=6m
5s～7s时间内因F3＞mg，所以电梯做向下的匀减速运动，
由牛顿第二定律得：F3-mg=ma3
代入数据解之得 a3=1m/s2
由公式x=v0t+
| 1 |
| 2 |
减速运动的位移为：x3=v1t3-
| 1 |
| 2 |
| t | 23 |
这段时间内电梯下降的距离X=x1+x2+x3=10m
答：（1）下楼
（2）在这段时间内电梯运动的距离是10m．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一质量m=40kg的物体在水平推力F作用下，沿水平地面向右运动．已知F=100N，物体与水平地面之间的动摩擦因数μ=0.2．物体经过某位置A的速度为v0=1.0m/s，此后物体再移动x=3.0m到达位置B．不计空气阻力，取g=10m/s2．求：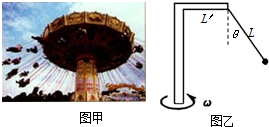
图甲为游乐场的悬空旋转椅，我们把这种情况抽象为图乙的模型：一质量m=40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上，水平杆长L′=7.5m．整个装置绕竖直杆转动，绳子与竖直方向成θ角．当θ=37°时，（g=9.8m/s2，sin37°=0.6，cos37°=0.8）求：
一质量m=40kg的小孩站在竖直电梯内的体重计上．电梯从t=0时刻由静止开始启动，在0到7s内体重计示数F的变化如图所示．试问：
角。当θ =37°时，（g = 9.8m/s2，sin37°= 0.6，cos37°= 0.8）求：