题目内容
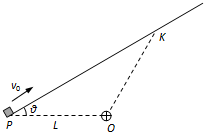 如图所示,粗糙程度均匀的固定绝缘平板下方O点有一电荷量为+Q的固定点电荷.一质量为m,电荷量为-q的小滑块以初速度v0从P点冲上平板,到达K点时速度恰好为零.已知O、P相距L,连线水平,与平板夹角为θ.O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件
如图所示,粗糙程度均匀的固定绝缘平板下方O点有一电荷量为+Q的固定点电荷.一质量为m,电荷量为-q的小滑块以初速度v0从P点冲上平板,到达K点时速度恰好为零.已知O、P相距L,连线水平,与平板夹角为θ.O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件| 2gLsin2θ |
| 4gLsin2θ |
(1)若小滑块刚冲上P点瞬间加速度为零,求小滑块与平板间滑动摩擦系数;
(2)求从P点冲到K点的过程中,摩擦力对小滑块做的功;
(3)满足(1)的情况下,小滑块到K点后能否向下滑动?若能,给出理由并求出其滑到P点时的速度;若不能,给出理由并求出其在K点受到的静摩擦力大小.
分析:对滑块受力分析,并沿x和y方向正交分解,列式可求小滑块与平板间动摩擦因数;
P、K两点距Q距离相等,故两点处电势相等.滑块从P到K电场做功为零,根据动能定理结合结合关系可求得摩擦力做功;
在k点,对滑块受力分析,分析比较可知,滑块会向下滑动,上下两个过程中摩擦力对滑块做的功相等,电场力做功为零,根据动能定理可求到p点的速度
P、K两点距Q距离相等,故两点处电势相等.滑块从P到K电场做功为零,根据动能定理结合结合关系可求得摩擦力做功;
在k点,对滑块受力分析,分析比较可知,滑块会向下滑动,上下两个过程中摩擦力对滑块做的功相等,电场力做功为零,根据动能定理可求到p点的速度
解答: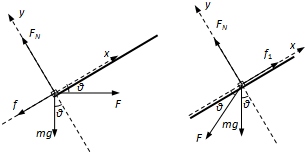 解:(1)刚冲上平板时库仑力大小为F,受力如图1,在x、y方向上分别有Fcosθ-mgsinθ-f=0
解:(1)刚冲上平板时库仑力大小为F,受力如图1,在x、y方向上分别有Fcosθ-mgsinθ-f=0
FN-mgcosθ-Fsinθ=0
其中f=μFN
F=k
得μ=
(2)P、K两点距Q距离相等,故两点处电势相等.
滑块从P到K电场做功为零
从P到K,对滑块-mgh+Wf=0-
m
由几何关系知,其中h=2Lcosθsinθ=Lsin2θ
得Wf=mgLsin2θ-
m
(3)在K点,库仑力大小仍为F,设滑块能保持静止,受力如图2,
在x、y方向分别有f1-mgsinθ-Fcosθ=0FN-mgcosθ-Fsinθ=0
解得,f1=mgsinθ+Fcosθ
而fm=μFN=Fcosθ-mgsinθ
因f1>fm,故滑块会向下滑动
下滑过程中,任意位置正压力都和上升时经过同一位置的正压力相等,故上下两个过程中摩擦力对滑块做的功相等.即Wf1=Wf
同样地,下滑到P点过程中,电场力做功为零,即mgh+Wf1=
m
-0
得v1=
由题目所给v0条件可知v1大于零,即滑块确能到达P点.
答:(1)小滑块与平板间滑动摩擦系数为
(2)从P点冲到K点的过程中,摩擦力对小滑块做的功为mgLsin2θ-
m
(3)满足(1)的情况下,小滑块到K点后能向下滑动,滑到P点时的速度为
,由题目所给v0条件可知v1大于零,即滑块确能到达P点
 解:(1)刚冲上平板时库仑力大小为F,受力如图1,在x、y方向上分别有Fcosθ-mgsinθ-f=0
解:(1)刚冲上平板时库仑力大小为F,受力如图1,在x、y方向上分别有Fcosθ-mgsinθ-f=0FN-mgcosθ-Fsinθ=0
其中f=μFN
F=k
| L2 |
得μ=
| kQqcosθ-mgL2sinθ |
| kQqsinθ+mgL2cosθ |
(2)P、K两点距Q距离相等,故两点处电势相等.
滑块从P到K电场做功为零
从P到K,对滑块-mgh+Wf=0-
| 1 |
| 2 |
| v | 2 0 |
由几何关系知,其中h=2Lcosθsinθ=Lsin2θ
得Wf=mgLsin2θ-
| 1 |
| 2 |
| v | 2 0 |
(3)在K点,库仑力大小仍为F,设滑块能保持静止,受力如图2,
在x、y方向分别有f1-mgsinθ-Fcosθ=0FN-mgcosθ-Fsinθ=0
解得,f1=mgsinθ+Fcosθ
而fm=μFN=Fcosθ-mgsinθ
因f1>fm,故滑块会向下滑动
下滑过程中,任意位置正压力都和上升时经过同一位置的正压力相等,故上下两个过程中摩擦力对滑块做的功相等.即Wf1=Wf
同样地,下滑到P点过程中,电场力做功为零,即mgh+Wf1=
| 1 |
| 2 |
| v | 2 1 |
得v1=
4gLsin2θ-
|
由题目所给v0条件可知v1大于零,即滑块确能到达P点.
答:(1)小滑块与平板间滑动摩擦系数为
| kQqcosθ-mgL2sinθ |
| kQqsinθ+mgL2sinθ |
(2)从P点冲到K点的过程中,摩擦力对小滑块做的功为mgLsin2θ-
| 1 |
| 2 |
| v | 2 0 |
(3)满足(1)的情况下,小滑块到K点后能向下滑动,滑到P点时的速度为
4gLsin2θ-
|
点评:本题考查了对带电小球的受力分析能力以及摩擦力做功的特点,知道库伦力跟距离的关系,难度适中

练习册系列答案
相关题目
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度V1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为V2(V2<V1)。若小物体电荷量保持不变,OM=ON,则
A.小物体上升的最大高度为 |
| B.从N到M的过程中,小物体的电势能逐渐减小 |
| C.从M到N的过程中,电场力对小物体先做负功后做正功 |
| D.从N到M的过程中,小物体受到的摩擦力和电场力均是先增大后减小 |
 (2009?四川)如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度V1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为V2(V2<V1).若小物体电荷量保持不变,OM=ON,则( )
(2009?四川)如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度V1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为V2(V2<V1).若小物体电荷量保持不变,OM=ON,则( ) 如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度V1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为V2(V2<V1).若小物体电荷量保持不变,OM=ON,则( )
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度V1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为V2(V2<V1).若小物体电荷量保持不变,OM=ON,则( ) . 若小物体电荷量保持不变,OM=ON,则( )
. 若小物体电荷量保持不变,OM=ON,则( )
