��Ŀ����
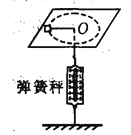
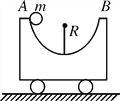
����Ŀ������Ƭ���ܳ�û����������һ����ڣ�ij���ܴ���ܶ����˹�ͷǿ��Ƶ����壬���������ϣ���ͼ����ʾ�����������ܴ������һ���취�����Լ����ܶ�������ʹ�����ѴӶ��þȣ�����̿ɼ���ͼ����ʾ��ģ�ͣ�������ΪO����ظ߶�ΪH��6m�����ܿ���Ϊ�ʵ���������m��500kg������ΪA�����¹������ĵ�����ľ���l��2m�ұ��ֲ��䣬�����ܳ��ܵ��������ΪFT��104N����ͷǿλ�ھ���O��ˮƽ����s��5m��B�㴦������һ����������ij���ܴ���ܶ��պ������Ұڵ���͵�ʱ����ǡ�ö��ѣ�������Ա������ţ�����������У�
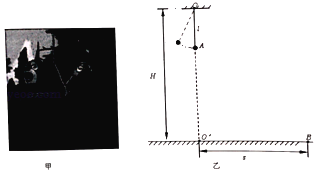
��1������ǡ�ö���˲���ܴ���ܶ����ٶ�Ϊ���
��2�����ǵ���ص����ͷǿ�ľ���Ϊ���٣�
��3�����ǵ����ʱ���ٶ�Ϊ���
���𰸡���1��2![]() m/s��2��1m��3��10m/s
m/s��2��1m��3��10m/s
��������
��1������͵�ʱ����ǡ�ö��ѣ�FT��104N������ţ�ٵڶ����ɵã�
FT��mg��m![]()
�ɵã�v��2![]() m/s
m/s
��2����ƽ���˶��ã�H��l![]() gt2
gt2
���![]()
ˮƽλ��Ϊ��x0��vt
���ǵ���ص����ͷǿ�ľ���Ϊ��d��s��x0
�����ã�d��1m
��3����ƽ���˶����ɿ�֪��vy��gt��4![]() m/s
m/s
���ǵ����ʱ���ٶ�Ϊ��v��![]() 10m/s
10m/s

��ϰ��ϵ�д�
�����Ŀ