题目内容
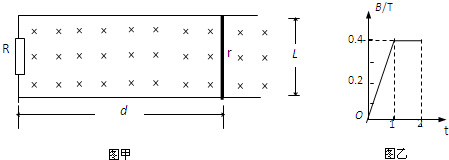
(2012?潮州二模)如图甲所示,在水平面上固定有宽为L=1.0m足够长的金属平行导轨,导轨左端接有的R=0.5Ω的电阻,垂直于导轨平面有一磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,在距导轨左端d=5m处有一阻值r=0.5Ω光滑导体棒,放置在导轨上,第1S内导体棒在一变力作用下始终处于静止状态,不计导体棒与导轨之间的接触电阻.求
(1)第1s内的感应电动势大小;
(2)第1s末拉力的大小及方向;
(3)若1s后拉力保持与第1s末相同,求导体棒的最终速度.
(1)第1s内的感应电动势大小;
(2)第1s末拉力的大小及方向;
(3)若1s后拉力保持与第1s末相同,求导体棒的最终速度.

分析:(1)根据法拉第电磁感应定律求出第1内产生的感应电动势大小.
(2)根据闭合电路欧姆定律求出电路中的电流,从而求出安培力的大小,根据楞次定律得出感应电流的方向,从而根据左手定则得出安培力的方向,拉力与安培力大小相等,方向相反.
(3)1s后导体棒做变加速直线运动,当拉力等于安培力时速度最大,根据切割产生的感应电动势,结合闭合电路欧姆定律,抓住合力为零,求出最终的速度.
(2)根据闭合电路欧姆定律求出电路中的电流,从而求出安培力的大小,根据楞次定律得出感应电流的方向,从而根据左手定则得出安培力的方向,拉力与安培力大小相等,方向相反.
(3)1s后导体棒做变加速直线运动,当拉力等于安培力时速度最大,根据切割产生的感应电动势,结合闭合电路欧姆定律,抓住合力为零,求出最终的速度.
解答:解:(1)第1s内由电磁感应定律可得:
电动势为E=
=Ld
=2V.
(2)由闭合电路欧姆定律知I=
=2A
F安=BIL=0.8N
由平衡条件知F=F安=0.8N
由楞次定律可得,感应电流的方向为逆时针方向,根据左手定则,导体棒安培力的方向水平向左,则拉力方向水平向右.
(3)1s后导体棒做变加速直线运动,当受力平衡速度达最大
则由电磁感应定律E′=BLv
由闭合电路欧姆定律知I′=
.
由平衡条件知F′=F安′=I′LB
联立解得v=
代入数据得V=5m/s.
答:(1)第1s内的感应电动势大小为2V.
(2)第1s末拉力的大小为0.8N,方向水平向右.
(3)导体棒的最终速度为5m/s.
电动势为E=
| △Φ |
| △t |
| △B |
| △t |
(2)由闭合电路欧姆定律知I=
| E |
| R+r |
F安=BIL=0.8N
由平衡条件知F=F安=0.8N
由楞次定律可得,感应电流的方向为逆时针方向,根据左手定则,导体棒安培力的方向水平向左,则拉力方向水平向右.
(3)1s后导体棒做变加速直线运动,当受力平衡速度达最大
则由电磁感应定律E′=BLv
由闭合电路欧姆定律知I′=
| E′ |
| R+r |
由平衡条件知F′=F安′=I′LB
联立解得v=
| F′(R+r) |
| B2L2 |
代入数据得V=5m/s.
答:(1)第1s内的感应电动势大小为2V.
(2)第1s末拉力的大小为0.8N,方向水平向右.
(3)导体棒的最终速度为5m/s.
点评:本题考查了切割产生感应电动势以及感生产生电动势,关键掌握产生电动势的公式,结合闭合电路欧姆定律和共点力平衡进行求解.

练习册系列答案
相关题目
 (2012?潮州二模)有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿圆台形表演台的侧壁,做匀速圆周运动.右图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h,下列说法中正确的是( )
(2012?潮州二模)有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿圆台形表演台的侧壁,做匀速圆周运动.右图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h,下列说法中正确的是( ) (2012?潮州二模)如图所示,电场中一正离子只受电场力作用从A点运动到B点.离子在A点的速度大小为v0,速度方向与电场方向相同.能定性反映该离子从A点到B点运动情况的速度-时间(v-t)图象是( )
(2012?潮州二模)如图所示,电场中一正离子只受电场力作用从A点运动到B点.离子在A点的速度大小为v0,速度方向与电场方向相同.能定性反映该离子从A点到B点运动情况的速度-时间(v-t)图象是( ) (2012?潮州二模)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态沿图线由A到B的过程,下列说法中正确的是( )
(2012?潮州二模)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态沿图线由A到B的过程,下列说法中正确的是( )