题目内容
18. 如图所示,在固定的水平绝缘平板上有A、B、C三点,B点左侧的空间存在着场强大小为E,方向水平向右的匀强电场,在A点放置一个质量为m,带正电的小物块,物块与平板之间的动摩擦因数为μ,若物块获得一个水平向左的初速度v0之后,该物块能够到达C点并立即折回,最后又回到A点静止下来.求:
如图所示,在固定的水平绝缘平板上有A、B、C三点,B点左侧的空间存在着场强大小为E,方向水平向右的匀强电场,在A点放置一个质量为m,带正电的小物块,物块与平板之间的动摩擦因数为μ,若物块获得一个水平向左的初速度v0之后,该物块能够到达C点并立即折回,最后又回到A点静止下来.求:(1)此过程中物块所走的总路程s有多大?
(2)若进一步知道物块所带的电量是q,那么B、C两点之间的距离是多大?
(3)若ab=L,那么物块第一次到达B点得速度是多大?
分析 (1)对全程应用动能定理有,摩擦力做的总功等于动能的变化量,摩擦力的功等于摩擦力与路程的乘积;
(2)对于小物块从A→C的过程应用动能定理,摩擦力与电场力所做的负功之和等于动能的减少量
(3)根据动能定理求的到达B点的速度
解答 解:(1)对全程应用动能定理,有:
-μmgs=0-$\frac{1}{2}$mv02,解得:s=$\frac{{v}_{0}^{2}}{2μg}$;
(2)设B、C两点之间的距离是l,对于小物块从A→C的过程应用动能定理有:
-μmg×$\frac{s}{2}$-qEl=0-$\frac{1}{2}$mv02,解得:l=$\frac{{mv}_{0}^{2}}{4qE}$;
(3)根据动能定理可得$-μmgL=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{0}^{2}$
解得$v=\sqrt{{v}_{0}^{2}-2μgL}$
答:(1)此过程中物块所走的总路程s为 $\frac{{v}_{0}^{2}}{2μg}$.
(2)若进一步知道物块所带的电量是q,那么B、C两点之间的距离是 $\frac{{mv}_{0}^{2}}{4qE}$.
(3)若ab=L,那么物块第一次到达B点得速度是$\sqrt{{v}_{0}^{2}-2μgL}$
点评 摩擦力的功等于摩擦力与路程的乘积;应用动能定理时要注意功的正负,并恰当选择好研究过程

练习册系列答案
相关题目
8.某物体在恒力作用下,从静止开始做直线运动,若t表示时间,l表示位移,则物体的动能( )
| A. | 与t成正比 | B. | 与t2成正比 | C. | 与l成正比 | D. | 与l2成正比 |
9.一本书静止放在水平桌面上,如图所示,下列说法中正确的是( )


| A. | 书对桌面的压力和桌面对书的支持力是一对平衡力 | |
| B. | 书所受重力和桌面对书的支持力是一对作用力和反作用力 | |
| C. | 书对桌面的压力是由于书的形变而产生的 | |
| D. | 书对桌面的压力就是书的重力 |
3.在离地面80m处无初速释放一小球,小球质量为m=200g,不计空气阻力,g取10m/s2,取地面为参考平面,求:
(1)前2s重力做的功;
(2)2s末重力的瞬时功率;
(3)在第2s末小球的重力势能.
(1)前2s重力做的功;
(2)2s末重力的瞬时功率;
(3)在第2s末小球的重力势能.
8.汽车通过一座拱桥,拱桥半径为25m,汽车的质量为10kg,当通过顶点的速度为5m/s时,汽车对拱桥的压力是多少(取g=10m/s2)( )
| A. | 100N | B. | 90N | C. | 25N | D. | 10N |
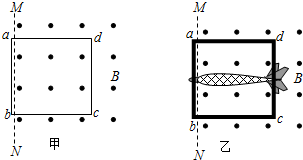 电磁弹射是我国最新研究的重大科技项目,原理可用下述模型说明.如图甲所示,虚线MN右侧存在一个竖直向上的匀强磁场,一边长L的正方形单匝均匀金属线框abcd放在光滑水平面上,电阻为R,质量为m,ab边在磁场外侧紧靠MN虚线边界.t=0时起磁感应强度B随时间t的变化规律是B=kt(k为大于零的常数),同时用一水平外力使线圈处于静止状态,空气阻力忽略不计.
电磁弹射是我国最新研究的重大科技项目,原理可用下述模型说明.如图甲所示,虚线MN右侧存在一个竖直向上的匀强磁场,一边长L的正方形单匝均匀金属线框abcd放在光滑水平面上,电阻为R,质量为m,ab边在磁场外侧紧靠MN虚线边界.t=0时起磁感应强度B随时间t的变化规律是B=kt(k为大于零的常数),同时用一水平外力使线圈处于静止状态,空气阻力忽略不计.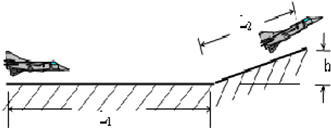
 一个物块由静止开始沿不同长度的光滑斜面滑到水平地面上的定点B,这些斜面的起点都靠在竖直墙上,如图所示,已知B点距离墙角距离为b,要使小物块从斜面的起点滑到B点所用的时间最短,求斜面的起点(如图中P点)距地面的高度是多少?所用的时间有是多少?
一个物块由静止开始沿不同长度的光滑斜面滑到水平地面上的定点B,这些斜面的起点都靠在竖直墙上,如图所示,已知B点距离墙角距离为b,要使小物块从斜面的起点滑到B点所用的时间最短,求斜面的起点(如图中P点)距地面的高度是多少?所用的时间有是多少?