题目内容
如图所示，一倾角为45°的斜面固定于竖直墙上，为使一光滑的铁球静止，需加一水平力F，且F过球心，下列说法正确的是（ ）分析：由题意可知，小球处于平衡状态；则可知小球所受各力的合力为零；对小球进行受力分析，小球受重力、推力、竖直墙的支持力及斜面对小球的支持力；可采用分解法将斜面支持力向水平方向和竖直方向分解，分别列出水平和竖直方向上的平衡方程，分情况进行讨论即可求解．
解答：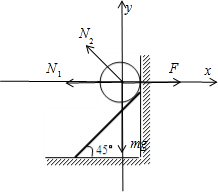
解：A、对小球进行受分析，如图所示：
若压力F等于N2水平向上的分力时，小球对竖直面没有压力，故N1有可能为零，
若压力F大于N2水平向上的分力时，球受墙的弹力且水平向左，故A错误，B正确；
C、若N2等于零，则小球受重力、推力F、竖直墙壁对小球向左的支持力，这三个力合力不可能为零，所以球一定受斜面的弹力且垂直斜面向上，故C正确，D错误；
故选B、C．
解：A、对小球进行受分析，如图所示：若压力F等于N2水平向上的分力时，小球对竖直面没有压力，故N1有可能为零，
若压力F大于N2水平向上的分力时，球受墙的弹力且水平向左，故A错误，B正确；
C、若N2等于零，则小球受重力、推力F、竖直墙壁对小球向左的支持力，这三个力合力不可能为零，所以球一定受斜面的弹力且垂直斜面向上，故C正确，D错误；
故选B、C．
点评：在解答平衡类的问题时，在注意准确的进行受力分析；而物体处于平衡状态时是指物体所受合力为零，若力为三个一般采用合成的方式，若力为三个以上，一般采用正交分解的方式，列出平衡方程即可求解．
练习册系列答案
相关题目
（2010?闵行区三模）如图所示，一倾角为37°的斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达C点时速度为零．每隔0.2s通过速度传感器测得物体的瞬时速度，下表给出了部分测量数据．（取 sin37°=0.6．cos37°=0.8）试求：
（2011?普陀区二模）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达最高点C．每隔0.2s通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据．（取sin37°=0.6，cos37°=0.8）（14分）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F。此后，物体到达最高点C。每隔0.2秒通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据。（取sin37°=0.6，cos37°=0.8）
| t/s | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
| V/ms-1 | 0.0 | 1.0 | 2.0 |
| 0.1 | 0.5 | 0.9 |
试求：（1）恒力F的大小；
（2）0.6秒时物体的瞬时速度；
（3）物体在斜面上运动过程中重力的最大功率；
（4）物体在斜面上运动的过程中，地面对斜面的摩擦力
（14分）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F。此后，物体到达最高点C。每隔0.2秒通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据。（取sin37°=0.6，cos37°=0.8）
| t/s | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
| V/ms-1 | 0.0 | 1.0 | 2.0 | | 0.1 | 0.5 | 0.9 |
试求：（1）恒力F的大小；
（2）0.6秒时物体的瞬时速度；
（3）物体在斜面上运动过程中重力的最大功率；
（4）物体在斜面上运动的过程中，地面对斜面的摩擦力
（14分）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F。此后，物体到达最高点C。每隔0.2秒通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据。（取sin37°=0.6，cos37°=0.8）
|
t/s |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
|
V/ms-1 |
0.0 |
1.0 |
2.0 |
|
0.1 |
0.5 |
0.9 |
试求：（1）恒力F的大小；
（2）0.6秒时物体的瞬时速度；
（3）物体在斜面上运动过程中重力的最大功率；
（4）物体在斜面上运动的过程中，地面对斜面的摩擦力