题目内容
在水平光滑直导轨上,静止放着三个质量均为m=1 kg的相同小球A、B、C.现让A球以v0=2 m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1 m/s.求:
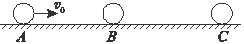
(1)A、B两球跟C球相碰前的共同速度为多大?
(2)两次碰撞过程中一共损失了多少动能?
【答案】
(1)1 m/s(2) 1.25 J
【解析】本题考查动量守恒定律,首先判断碰撞前后动量守恒,碰撞后粘合为一个整体,列式求解
(1)A、B相碰满足动量守恒:
mv0=2mv1 2分
得两球跟C球相碰前的速度v1=1 m/s 1分
(2)两球与C碰撞同样满足动量守恒:2mv1=mvC+2mv2 2分
得两球碰后的速度v2=0.5 m/s.
两次碰撞过程中一共损失的动能为
ΔEk=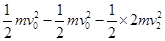 2分
2分
ΔEk=1.25 J 1分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
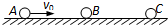 【选修3-5】如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,碰后C球的速度vC=1m/s.求:
【选修3-5】如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,碰后C球的速度vC=1m/s.求: 物理--选修3-5
物理--选修3-5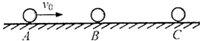 如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C,现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.求A、B两球跟C球相碰前的速度和相碰后的速度.
如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C,现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.求A、B两球跟C球相碰前的速度和相碰后的速度. (选修模块3-5)
(选修模块3-5) 合在一起继续向右运动,再跟C球碰撞,C球的最终速度为vC=1m/s.求:
合在一起继续向右运动,再跟C球碰撞,C球的最终速度为vC=1m/s.求: