题目内容
【题目】如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为T。现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为1∶3。
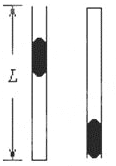
(1)将管内气体加热,至水银面上端与管口相平,求此时气体的温度T1
(2)若将管内下部气体温度降至![]() ,在保持温度T2不变,将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出)。已知大气压强为
,在保持温度T2不变,将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出)。已知大气压强为![]() ,重力加速度为
,重力加速度为![]() 。求水银柱的长度
。求水银柱的长度![]() 和水银的密度
和水银的密度![]() 。
。
【答案】(1) ![]() (2)
(2) ![]() ,
, ![]()
【解析】试题分析:找出初末态的参量,气体发生等压变化,根据盖-吕萨克定律即可求解;找出状态参量,根据理想气体状态方程即可求解。
(1)设细管横截面积为s,初末态的体积关系为:![]()
气体等压膨胀,根据盖-吕萨克定律:![]()
解得:![]()
(2)细管注入水银后下部气体压强为![]()
体积为![]()
注入水银过程,由玻意耳定律有: ![]()
将管倒置后,管内气体压强为![]()
解得体积为:![]()
由理想气体状态方程有: ![]()
解得:![]()
![]()

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目