题目内容
6.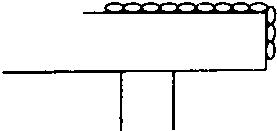 如图所示,在光滑的桌面上有一根均匀柔软的质量为m,长度为l的绳子,绳子的$\frac{1}{4}$悬于桌面下,从绳子开始下滑至绳子刚好全部离开桌面的过程中,重力对绳子做功为多少?绳子的重力势能变化量为多少?(桌面离底面高度大于l).
如图所示,在光滑的桌面上有一根均匀柔软的质量为m,长度为l的绳子,绳子的$\frac{1}{4}$悬于桌面下,从绳子开始下滑至绳子刚好全部离开桌面的过程中,重力对绳子做功为多少?绳子的重力势能变化量为多少?(桌面离底面高度大于l).
分析 可取桌面为零势能面,将绳子分为桌上的部分和桌下的部分,分别确定出其两种情况下的重力势能,然后得到其变化量.再由功能关系确定重力所做的功.
解答 解:设桌面为零势能面,开始时绳子的重力势能为:E1=-$\frac{1}{4}$mg•$\frac{1}{8}$l=-$\frac{1}{32}$mgl
当链条刚脱离桌面时的重力势能:E2=-mg•$\frac{1}{2}$l=-$\frac{1}{2}$mgl
故重力势能的变化量:△EP=E2-E1=-$\frac{15}{32}$mgl;
而重力做功等于重力势能的改变量;重力势能减小,说明重力做正功;
故重力做功W=-△EP=$\frac{15}{32}$mgl;
答:重力对绳子做功为$\frac{15}{32}$mgl;绳子的重力势能变化量为-$\frac{15}{32}$mgl.
点评 零势能面的选取是任意的,本题也可以选链条滑至刚刚离开桌边时链条的中心为零势能面,结果是一样的,要注意重力势能的正负.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 对一定质量的理想气体,温度越低,其内能越小 | |
| B. | 物体吸收热量的同时又对外做功,其内能可能增加 | |
| C. | 热力学第二定律可描述为“热量不可能由低温物体传递到高温物体” | |
| D. | 悬浮在液体中的微粒越大,在某一瞬间跟它相撞的液体分子就越多,布朗运动越明显 | |
| E. | 一定质量的气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加 |
15.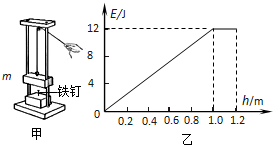 如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )
如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )
 如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )
如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )| A. | 物块在F作用下向上运动的加速度为12 m/s2 | |
| B. | 物块上升过程的最大速度为2$\sqrt{6}$m/s | |
| C. | 物块上升到0.25m高度处拉力F的瞬时功率为12W | |
| D. | 铁钉被打入10cm深度的过程中受到的平均阻力为112N |
 “理光牌”复印机的偏转电场如图所示,电容器的电容为C,板长为L,两极板间距为d,现有一个带电量为q,质量为m的墨粉微粒,以初速度v0沿两极板的中线垂直电场进入偏转电场中,若墨粉微粒恰能从极板边缘射出电场(不计重力),求:
“理光牌”复印机的偏转电场如图所示,电容器的电容为C,板长为L,两极板间距为d,现有一个带电量为q,质量为m的墨粉微粒,以初速度v0沿两极板的中线垂直电场进入偏转电场中,若墨粉微粒恰能从极板边缘射出电场(不计重力),求: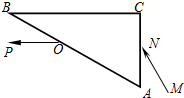 如图所示,△ABC为直角三棱镜的横截面,∠ABC=30°.有一细光束MN射到AC面上,且MN与AC的夹角也为30°,该光束从N点进入棱镜后再经BC面反射,最终从AB面上的O点射出,其出射光线OP与BC面平行.
如图所示,△ABC为直角三棱镜的横截面,∠ABC=30°.有一细光束MN射到AC面上,且MN与AC的夹角也为30°,该光束从N点进入棱镜后再经BC面反射,最终从AB面上的O点射出,其出射光线OP与BC面平行.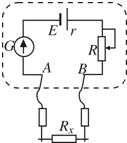 如图所示为一简单欧姆表原理示意图,其中电流表G的满偏电流Ig=300μA,内阻Rg=100Ω,可变电阻R的最大阻值为10kΩ,电池的电动势E=1.5V,内阻r=0.5Ω,图中与接线柱A相连的表笔颜色应是红色.按正确使用方法测量电阻Rx的阻值时,指针指在刻度盘的正中央,则Rx=5 kΩ.
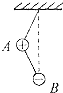
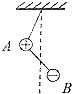
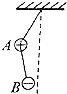
如图所示为一简单欧姆表原理示意图,其中电流表G的满偏电流Ig=300μA,内阻Rg=100Ω,可变电阻R的最大阻值为10kΩ,电池的电动势E=1.5V,内阻r=0.5Ω,图中与接线柱A相连的表笔颜色应是红色.按正确使用方法测量电阻Rx的阻值时,指针指在刻度盘的正中央,则Rx=5 kΩ.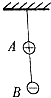 如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )
如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )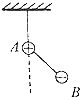
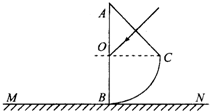 如图所示为某种透明介质的截面图,△AOC为等腰直角三角形,BC为半径R=12cm的四分之一圆弧,AB与水平屏幕MN垂直接触于B点.由红光和紫光两种单色光组成的复色光垂直AC射到O,结果在水平屏幕MN上出现两个亮斑.已知该介质对红光和紫光的折射率分别为n1=$\frac{2\sqrt{3}}{3}$,n2=$\sqrt{2}$.
如图所示为某种透明介质的截面图,△AOC为等腰直角三角形,BC为半径R=12cm的四分之一圆弧,AB与水平屏幕MN垂直接触于B点.由红光和紫光两种单色光组成的复色光垂直AC射到O,结果在水平屏幕MN上出现两个亮斑.已知该介质对红光和紫光的折射率分别为n1=$\frac{2\sqrt{3}}{3}$,n2=$\sqrt{2}$.