题目内容
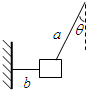 如图所示,用一根绳子a把物体挂起来,再用一根水平的绳子b把物体拉向一旁固定起来.物体的重量是40N,绳子a与竖直方向的夹角θ=30°,绳子a和b对物体的拉力分别是多大?
如图所示,用一根绳子a把物体挂起来,再用一根水平的绳子b把物体拉向一旁固定起来.物体的重量是40N,绳子a与竖直方向的夹角θ=30°,绳子a和b对物体的拉力分别是多大?分析:以物体为研究对象,分析受力情况,作出力图,根据平衡条件采用正交分解法求解.
解答: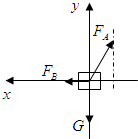 解:以物体为研究对象进行受力分析,作出力图如图所示.
解:以物体为研究对象进行受力分析,作出力图如图所示.
设绳子A对物体的拉力大小为FA,绳子B对物体的拉力大小为FB:
以水平方向为x轴,竖直方向为y轴建立直角坐标系,
由共点力的平衡条件得:
FB-FAsin30°=0 ①
FAcos30°-G=0 ②
代入数据联立求解①②得
FA=
N,FB=
N
答:绳子a和b对物体的拉力分别是FA=
N,FB=
N.
 解:以物体为研究对象进行受力分析,作出力图如图所示.
解:以物体为研究对象进行受力分析,作出力图如图所示.设绳子A对物体的拉力大小为FA,绳子B对物体的拉力大小为FB:
以水平方向为x轴,竖直方向为y轴建立直角坐标系,
由共点力的平衡条件得:
FB-FAsin30°=0 ①
FAcos30°-G=0 ②
代入数据联立求解①②得
FA=
80
| ||
| 3 |
40
| ||
| 3 |
答:绳子a和b对物体的拉力分别是FA=
80
| ||
| 3 |
40
| ||
| 3 |
点评:本题是简单的力平衡问题,采用的是正交分解法处理的,也可以应用合成法或分解法求解.

练习册系列答案
相关题目
 如图所示,用一根绳子a把物体挂起来,再用另一根水平的绳子b 把物体拉向一旁固定起来.物体的重力是40N,绳子a与竖直方向的夹角θ=37°,绳子a与b对物体的拉力分别是多大?(sin37°=0.6,cos37°=0.8)
如图所示,用一根绳子a把物体挂起来,再用另一根水平的绳子b 把物体拉向一旁固定起来.物体的重力是40N,绳子a与竖直方向的夹角θ=37°,绳子a与b对物体的拉力分别是多大?(sin37°=0.6,cos37°=0.8)
 把物体挂起来,再用一根水平的绳子
把物体挂起来,再用一根水平的绳子 把物体拉向一旁固定起来. 物体的重量是40N,绳子
把物体拉向一旁固定起来. 物体的重量是40N,绳子 30°,绳子
30°,绳子