题目内容
一物块在粗糙水平面上，受到的水平拉力F随时间t变化如图（a）所示，速度v随时间t变化如图（b）所示（g=10m/s2）．求：
①1秒末物块所受摩擦力f的大小．
②物块质量m．
③物块与水平面间的动摩擦因数μ．
④若在6秒末撤去拉力F，物块通过的位移大小．
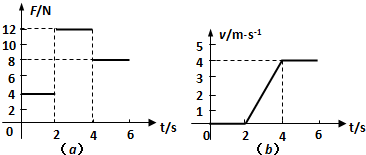
解：①从图（b）可知，前2s内物体静止不动，摩擦力等于拉力．图（a）中可以读出，当t=1s时，f1=F1=4N
②从图（b）中可以看出，当t=2s至t=4s过程中，物块做匀加速运动，加速度大小为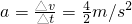
由牛顿第二定律，有F2-μmg=ma
物体在4-6s时间内做匀速直线运动，滑动摩擦力等于拉力，即：F3=f3=μmg
所以：
③由F3=f3=μmg得，
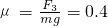
④2-4S物块通过位移大小：
m
4-6S物块通过移位大小：S2=vt=4×2m=8m
撤去F后物块加速度大小：
通过位移大小：
m
物块通的总位移：S=S1+S2+S3=14m
答：①1秒末物块所受摩擦力f的大小4N．
②物块质量2kg．
③物块与水平面间的动摩擦因数μ=0.4．
④若在6秒末撤去拉力F，物块通过的位移大小14m．
分析：通过（b）图可以知道物体的速度随时间的变化关系．再把牛顿第二定律结合（a）图可以对其他的未知条件进行分析与计算．
点评：该题以图象的方式考查受力分析与牛顿运动定律的应用，涉及的过程比较多，但都比较简单．属于中档题目．
②从图（b）中可以看出，当t=2s至t=4s过程中，物块做匀加速运动，加速度大小为
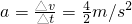
由牛顿第二定律，有F2-μmg=ma
物体在4-6s时间内做匀速直线运动，滑动摩擦力等于拉力，即：F3=f3=μmg
所以：
③由F3=f3=μmg得，
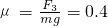
④2-4S物块通过位移大小：
m4-6S物块通过移位大小：S2=vt=4×2m=8m
撤去F后物块加速度大小：
通过位移大小：
m物块通的总位移：S=S1+S2+S3=14m
答：①1秒末物块所受摩擦力f的大小4N．
②物块质量2kg．
③物块与水平面间的动摩擦因数μ=0.4．
④若在6秒末撤去拉力F，物块通过的位移大小14m．
分析：通过（b）图可以知道物体的速度随时间的变化关系．再把牛顿第二定律结合（a）图可以对其他的未知条件进行分析与计算．
点评：该题以图象的方式考查受力分析与牛顿运动定律的应用，涉及的过程比较多，但都比较简单．属于中档题目．
练习册系列答案
相关题目
一物块在粗糙水平面上，受到的水平拉力F随时间t变化如图（a）所示，速度v随时间t变化如图（b）所示（g=10m/s2）．求：