题目内容
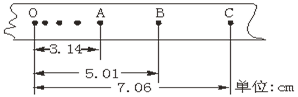
【题目】(17分)如图所示,水平轨道左端与长L=1.25m的水平传送带相接,传送带逆时针匀速运动的速度v0=1m/s。轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板上.竖直半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,g取10m/s2。求:

(1)物块到达B点时速度vB的大小;
(2)弹簧被压缩时的弹性势能EP;
(3)若长木板与水平地面间动摩擦因数0.016≤μ3≤0.026,要使小物块恰好不会从长木板上掉下,木板长度S的取值范围是多少 (设最大静动摩擦力等于滑动摩擦力)。
【答案】(1)2m/s (2)1.2J(3)3.27m≤s≤4m
【解析】
试题分析:(1)由牛顿第二定律得:![]() ,
,![]()
(2)物块被弹簧弹出的过程中,物块和弹簧组成的系统机械能守恒:![]()
![]()
![]() 物体在传送带上一直做匀减速运动
物体在传送带上一直做匀减速运动
物块在传送带上滑行过程由动能定理得:-![]() —
—![]()
![]()
![]()
联立解得:![]()
(3)物块从B到C过程中由机械能守恒定律得:mg2R=![]() mvC2
mvC2![]() mvB2,
mvB2,
联立解得:vC=2![]() m/s
m/s
讨论:Ⅰ.当μ3=0.016时,小物块恰好不会从长木板上掉下长度为s1,
小物块和长木板共速为v,物块的加速度为:a1=μ2g=2.5m/s2;木板的加速度为: ![]()
由vC-a1t=a2t可知,木块与木板共速时的时间为:t=1s
木板的长度为:![]() ,代入数据可知:s=3.27m
,代入数据可知:s=3.27m
Ⅱ.当μ3=0.026时,小物块恰好不会从长木板上掉下长度为s2,
物块在长木板上滑行过程中,对长木板受力分析:
上表面受到的摩擦力f2=μ2mg=0.25×1N=0.25N.
下表面受到的摩擦力f3≤μ3(M+m)g=0.026×10N=0.26N
所以长木板静止不动,对物块在长木板上滑行过程
由动能定理得:-f2s2=0![]() mvC2
mvC2
代入数据解得s2=4m
所以木板长度的范围是3.27m≤s≤4m

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案