题目内容
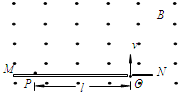如图所示，MN表示真空室中垂直于纸面放置的感光板，它的一侧有匀强磁场，磁场方向垂直于纸面向外，磁感应强度大小为B．一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域，最后到达感光板上的P点．经测量P、O间的距离为l，不计带电粒子受到的重力．求：（1）带电粒子所受洛伦兹力的大小；
（2）此粒子的质量大小；
（3）要想增大P、O间的距离为l，都可以想到哪些办法？
分析：（1）带电粒子所受洛伦兹力的大小由公式F=qvB求解．
（2）由图看出，带电粒子在磁场中做匀速圆周运动，运动半周垂直打在P点，其运动半径为r=
，带电粒子在磁场中由洛伦兹力提供向心力，由牛顿第二定律可求出质量．
（3）根据l=2r=
，分析要想增大l，可采用的办法．
（2）由图看出，带电粒子在磁场中做匀速圆周运动，运动半周垂直打在P点，其运动半径为r=
| l |
| 2 |
（3）根据l=2r=
| 2mv |
| qB |
解答：解：（1）带电粒子所受洛伦兹力的大小；f=qvB
（2）带电粒子在磁场中做匀速圆周运动，由图知，其轨迹半径为R=
由qvB=m
得
m=
=
（3）由上式可知，l=2r=
，则知要想增大P、O间的距离l，可增大速度v，或减小电荷量q等．
答：
（1）带电粒子所受洛伦兹力的大小为qvB；
（2）此粒子的质量大小是
；
（3）要想增大P、O间的距离为l，可增大速度v，或减小电荷量q等．
（2）带电粒子在磁场中做匀速圆周运动，由图知，其轨迹半径为R=
| l |
| 2 |
由qvB=m
| v2 |
| R |
m=
| qvBR |
| v2 |
| qBl |
| 2v |
（3）由上式可知，l=2r=
| 2mv |
| qB |
答：
（1）带电粒子所受洛伦兹力的大小为qvB；
（2）此粒子的质量大小是
| qBl |
| 2v |
（3）要想增大P、O间的距离为l，可增大速度v，或减小电荷量q等．
点评：本题是质谱仪，关键抓住洛伦兹力提供向心力，结合几何知识进行研究．
练习册系列答案
相关题目
如图所示，真空中M、N处放置两等量异号电荷，a、b、c表示电场中的3条等势线，d点和e点位于等势线a上，f点位于等势线c上，且df平行于MN．已知一带正电的试探电荷从d点移动到f点时，试探电荷的电势能增加，则以下判断正确的是（ ）
点电荷置于真空中的O点，A、B、C三个虚线圆表示该点电荷电场中三个等势面，如图所示．已知等势面的电势?A＜?B＜?C，m点位于A等势面上，n点位于B等势面上．现有一电子从m点以初速度v0沿mn方向入射，在电子从m点至再次通过A等势面的过程中，以下判断正确的是（ ）
如图所示，两等量异号点电荷分别置于真空中M、N处，a、b、c表示电场中的3条等势线，b是M、N连线的中垂线，交MN于O点，a、c关于b对称．点d、e、f、g是以O为圆心的圆与a、c的交点，已知一带正电的试探电荷从d点移到e点时，试探电荷的电势能增加，则以下判断正确的是（ ）| A、M点处放置的是正电荷 | B、d点的电势高于f点的电势 | C、d点的场强与f点的场强相同 | D、将带正电的试探电荷沿直线由d点移到f点，电势能先增大后减小 |
如图所示，真空中M、N处分别放置两等量异种电荷，a、b、c表示电场中的3条等势线，d点和e点位于a等势线上，f点位于c等势线上，df平行于MN．以下说法正确的是（ ）| A、d点的电势高于f点的电势 | B、d点的电势与e点的电势相等 | C、若将一负试探电荷沿直线由d点移动到f点，则电场力先做正功、后做负功 | D、若将一正试探电荷沿直线由d点移动到e点，试探电荷的电势能增加 |