题目内容
如图所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速度沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,在物块m上、下滑动的整个过程中( )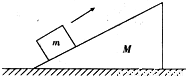
A.地面对斜劈M的摩擦力方向先向左后向右
B.地面对斜劈M的摩擦力方向没有改变
C.物块m向上、向下滑动时加速度大小相同
D.地面对斜劈M的支持力始终大于(M+m)g
【答案】分析:对物体m受力分析,根据牛顿第二定律判断加速度变化情况;对M与m整体受力分析,根据牛顿第二定律列式分析地面支持力和摩擦力变化情况.
解答:解:A、B、物体m先减速上升,后加速下滑,加速度一直沿斜面向下,对M与m整体受力分析,受到重力(M+m)g,地面支持力N,和地面摩擦力,根据牛顿第二定律,有
水平分析:f=m?(a?sinθ) ①
竖直方向:(M+m)g-N=m?(a?cosθ) ②
其中θ为斜面坡角
故地面对斜面体的静摩擦力方向没有改变,故A错误,B正确;
C、对m受力分析,受到重力、支持力、和滑动摩擦力
减速上滑时,有
f1+mgsinθ=ma1
加速下滑时,有
mgsinθ-f1=ma2
故a1>a2
故C错误;
D、由②式可知,N<(M+m)g,故D错误;
故选B.
点评:本题关键是对整体受力分析后根据牛顿第二定律列式求解出支持力和静摩擦力的表达式后进行分析讨论;整体法不仅适用与相对静止的物体系统,同样也适用与有相对运动的物体之间.
解答:解:A、B、物体m先减速上升,后加速下滑,加速度一直沿斜面向下,对M与m整体受力分析,受到重力(M+m)g,地面支持力N,和地面摩擦力,根据牛顿第二定律,有
水平分析:f=m?(a?sinθ) ①
竖直方向:(M+m)g-N=m?(a?cosθ) ②
其中θ为斜面坡角
故地面对斜面体的静摩擦力方向没有改变,故A错误,B正确;
C、对m受力分析,受到重力、支持力、和滑动摩擦力
减速上滑时,有
f1+mgsinθ=ma1
加速下滑时,有
mgsinθ-f1=ma2
故a1>a2
故C错误;
D、由②式可知,N<(M+m)g,故D错误;
故选B.
点评:本题关键是对整体受力分析后根据牛顿第二定律列式求解出支持力和静摩擦力的表达式后进行分析讨论;整体法不仅适用与相对静止的物体系统,同样也适用与有相对运动的物体之间.

练习册系列答案
相关题目
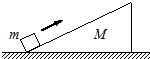 如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( )
如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( )| A、物块m向上滑动与向下滑动时加速度大小相同 | B、物块m向上滑动的时间小于向下滑动的时间 | C、地面对斜劈M的支持力大于(M+m)g | D、地面对斜劈M的摩擦力方向始终不变 |
 如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( )
如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( ) 如图所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速度沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,在物块m上、下滑动的整个过程中( )
如图所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速度沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,在物块m上、下滑动的整个过程中( ) 如图所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( )
如图所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中( ) 如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速度沿劈的斜面向上滑,至速度为零后又加速下滑,而M始终保持静止,则在物块m沿斜面上滑与下滑的过程中( )
如图所示,斜劈形物体的质量为M,放在水平地面上,质量为m的粗糙物块以某一初速度沿劈的斜面向上滑,至速度为零后又加速下滑,而M始终保持静止,则在物块m沿斜面上滑与下滑的过程中( )