题目内容
19.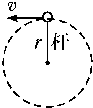 杆的一端固定,另一端系一质量为m=0.5kg的小球,杆长l=0.6m,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求:
杆的一端固定,另一端系一质量为m=0.5kg的小球,杆长l=0.6m,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求:(1)小球刚好能做圆周运动,在最高点的速度为多大?
(2)小球在最高点速率v=3m/s时,杆对小球的作用力为多大?
(3)小球在最低点速率v=$\sqrt{21}$m/s时,杆对小球的作用力为多大?
分析 当小球刚好做圆周运动,最高点的临界速度为零.当最高点的速度为3m/s和最低点速度为5m/s时,根据牛顿第二定律求出杆对小球的作用力大小.
解答 解:(1)小球刚好能做圆周运动,在最高点的速度为0,杆子的作用力等于重力,方向竖直向上.
(2)当最高点的速率v=3m/s时,根据牛顿第二定律得,mg+${F}_{1}=m\frac{{{v}_{1}}^{2}}{l}$,解得${F}_{1}=0.5×\frac{9}{0.6}-5=2.5N$.
(3)当最低点速度为v=$\sqrt{21}$m/s时,根据牛顿第二定律得,${F}_{2}-mg=m\frac{{{v}_{2}}^{2}}{l}$,解得${F}_{2}=5+0.5×\frac{21}{0.6}=22.5N$.
答:(1)小球刚好能做圆周运动,在最高点的速度为0.
(2)小球在最高点速率v=3m/s时,杆对小球的作用力为2.5N.
(3)小球在最低点速率v=$\sqrt{21}$m/s时,杆对小球的作用力为22.5N
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解,知道绳模型与杆模型的区别.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
9.下列现象中,不是由于液体的表面张力而引起的是( )
| A. | 小昆虫能在水面上自由走动 | |
| B. | 融化的蜡烛从燃烧的蜡烛上流下来,冷却后呈球形 | |
| C. | 小孩吹出肥皂泡 | |
| D. | 树叶能飘浮在水面上 |
10.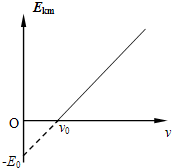 在做光电效应的实验时,某金属被光照射发生了光电效应,实验测得光电子的最大初动能EK与入射光的频率ν的关系如图所示,由实验图线可求出( )
在做光电效应的实验时,某金属被光照射发生了光电效应,实验测得光电子的最大初动能EK与入射光的频率ν的关系如图所示,由实验图线可求出( )
 在做光电效应的实验时,某金属被光照射发生了光电效应,实验测得光电子的最大初动能EK与入射光的频率ν的关系如图所示,由实验图线可求出( )
在做光电效应的实验时,某金属被光照射发生了光电效应,实验测得光电子的最大初动能EK与入射光的频率ν的关系如图所示,由实验图线可求出( )| A. | 普朗克常数 | B. | 该金属的逸出功 | ||
| C. | 该金属的截止频率 | D. | 单位时间内逸出的光电子数 |
7.关于功率,下列说法中正确的是( )
| A. | 力对物体做功越多,则力做功的功率越大 | |
| B. | 从公式P=Fv可知,汽车的牵引力一定跟汽车行驶的速率成反比 | |
| C. | 由公式P=$\frac{W}{t}$可知,物体做功时间越短,其功率越大 | |
| D. | 功率是描述物体做功快慢的物理量 |
14.一个质量为m、速度为v的物体沿半径为r的圆做匀速圆周运动,若它所受力的合力大小变为F,方向仍指向原来的圆心,则( )
| A. | 当F=$\frac{m{v}^{2}}{r}$时,物体将偏离原轨迹运动 | |
| B. | 当F<$\frac{m{v}^{2}}{r}$时,物体将靠近原来的圆心运动 | |
| C. | 当F>$\frac{m{v}^{2}}{r}$时,物体将远离原来的圆心运动 | |
| D. | 制作棉花糖时,利用了物体做离心运动的原理 |
4.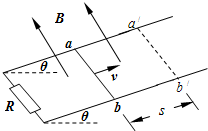 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{R}$ | |
| B. | 上滑过程中导体棒损失的机械能大小为μmgs cosθ | |
| C. | 上滑过程中电流做功发出的热量为$\frac{m{v}^{2}}{2}$-mgs (sinθ+μcosθ) | |
| D. | 上滑过程中安培力、滑动摩擦力和重力对导体棒做的总功为正$\frac{m{v}^{2}}{2}$ |
11.物体做匀速圆周运动,其线速度为v、角速度为ω、半径为r、周期为T.下列关系式中错误的是( )
| A. | ω=$\frac{2π}{T}$ | B. | ω=rv | C. | v=rω | D. | v=$\frac{2πr}{T}$ |
9.嫦娥工程划为三期,简称“绕、落、回”三步走.我国发射的“嫦娥三号”卫星是嫦娥工程第二阶段的登月探测器,经变轨成功落月.若该卫星在某次变轨前,在距月球表面高度为h的轨道上绕月球做匀速圆周运动,其运行的周期为T.若以R表示月球的半径,忽略月球自转及地球对卫星的影响,则( )
| A. | “嫦娥三号”绕月球做匀速圆周运动时的线速度大小为$\frac{2πR}{T}$ | |
| B. | 物体在月球表面自由下落的加速度大小为$\frac{{4{π^2}{{({R+h})}^3}}}{{R{T^2}}}$ | |
| C. | 月球的第一宇宙速度为$\frac{{2π({R+h})}}{T}\sqrt{\frac{R+h}{R}}$ | |
| D. | 月球的平均密度为$\frac{3π}{{G{T^2}}}$ |