题目内容
如图4-1-5所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三轮半径之间的关系为rA=rC=2rB.若皮带不打滑,求A、B、C轮边缘上的a、b、c三点的角速度之比和线速度之比.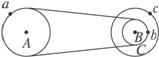
图4-1-5
解析:A、B两轮通过皮带传动,且皮带不打滑,则A、B两轮边缘的线速度大小相等,即va=vb
由v=ωr得ωa∶ωb=rB∶rA=1∶2
B、C两轮固定在一起绕同轴转动,则B、C两轮的角速度相等,即ωb=ωc,由v=ωr得
vb∶vc=rB∶rC=1∶2
由以上各式得ωa∶ωb∶ωc=1∶2∶2
va∶vb∶vc=1∶1∶2.
答案:1∶2∶2 1∶1∶2

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
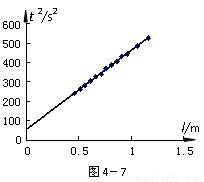
 d)图线。
d)图线。