题目内容
8. 如图所示,两平行金属导轨相距L=0.20m,与水平面夹角为θ=37°.在两金属导轨下端,用导线连接电源和定值电阻.电源电动势E=6.0V,内阻r=1.0Ω,定值电阻R=2.0Ω,其它电阻不计.金属棒MN的质量为m=0.10kg,刚好横放在两金属导轨上,且与导轨间的动摩擦因数为μ=0.50.整个装置处在垂直于轨道平面向上的匀强磁场中,设金属棒所受的最大静摩擦力等于滑动摩擦力.为使金属棒MN处于静止状态,磁感应强度B应该为多大?(g=10m/s2,sin37°=0.6,cos37°=0.8,计算结果均取两位有效数字)
如图所示,两平行金属导轨相距L=0.20m,与水平面夹角为θ=37°.在两金属导轨下端,用导线连接电源和定值电阻.电源电动势E=6.0V,内阻r=1.0Ω,定值电阻R=2.0Ω,其它电阻不计.金属棒MN的质量为m=0.10kg,刚好横放在两金属导轨上,且与导轨间的动摩擦因数为μ=0.50.整个装置处在垂直于轨道平面向上的匀强磁场中,设金属棒所受的最大静摩擦力等于滑动摩擦力.为使金属棒MN处于静止状态,磁感应强度B应该为多大?(g=10m/s2,sin37°=0.6,cos37°=0.8,计算结果均取两位有效数字)
分析 根据闭合电路欧姆定律求出电路中的电流大小,当磁感应强度最小时,金属棒所受的静摩擦力沿导轨向上,当磁感应强度最大时,金属棒所受的静摩擦力方向沿导轨向下,结合共点力平衡以及安培力的大小公式求出磁感应强度的范围.
解答 解:由闭合电路欧姆定律得电路中的电流为:
$I=\frac{E}{R+r}=\frac{6}{2+1}A=2.0A$,
由左手定则可判定金属棒受到的安培力沿斜面向上.当磁感应强度最小时,金属棒受到的静摩擦力方向沿导轨向上且达到最大.由平衡条件得:
BminIL-mgsinθ+μmgcosθ=0,
磁感应强度最小值为:
${B}_{min}=\frac{mg(sinθ-μcosθ)}{IL}$=$\frac{1×(0.6-0.5×0.8)}{2×0.2}=0.50T$,
当磁感应强度最大时,金属棒受到的静摩擦力方向沿导轨向下且达到最大.由平衡条件得:
BmaxIL-mgsinθ-μmgcosθ=0,
磁感应强度最大值为:
${B}_{max}=\frac{mg(μcosθ+sinθ)}{IL}$=$\frac{1×(0.5×0.8+0.6)}{2×0.2}=2.5T$,
为使金属棒MN处于静止状态,磁感应强度的大小应该为0.50T≤B≤2.5T
答:为使金属棒MN处于静止状态,磁感应强度0.50T≤B≤2.5T.
点评 本题考查了安培力与共点力平衡的综合运用,关键抓住两个临界状态,结合安培力公式和共点力平衡综合求解,难度中等.

练习册系列答案
相关题目
18.正常走动的钟表,其时针和分针都在做匀速转动,则下列关系中正确的是( )
| A. | 时针和分针角速度相同 | B. | 分针的周期是时针周期的12倍 | ||
| C. | 时针和分针的周期相同 | D. | 分针角速度是时针角速度的12倍 |
16.从作匀速直线运动的火车窗口释放一石子,不计风对石子运动的影响,站在路边的人和车上的人看到石子分别作( )
| A. | 自由落体运动和平抛运动 | B. | 平抛运动和自由落体运动 | ||
| C. | 匀速直线运动和自由落体运动 | D. | 匀变速直线运动和自由落体运动 |
20. 一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
 一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )| A. | 第1s末物体的位移和速度都不改变方向 | |
| B. | 第2s末物体的加速度和速度都改变方向 | |
| C. | 前4s内物体的位移为零 | |
| D. | 第1s末、第3s末、第5s末物体的速度相同 |
18.物体自45m高处做自由落体运动,从开始下落算起,第1s末、第2s末、第3s末的速度之比是( )
| A. | 1:1:1 | B. | 1:2:3 | C. | 1:4:9 | D. | 3:2:1 |
 如图所示为光电计时器的实验简易示意图.当有不透光物体从光电门间通过时,光电计时器就可以显示物体的挡光时间.光滑水平导轨MN上放置两个相同的物块A和B,左端挡板处有一弹射装置P,右端N处与水平传送带平滑连接,今将挡光效果好,宽度为d=3.6×10-3 m的两块黑色磁带分别贴在物块A和B上,且高出物块,并使高出物块部分在通过光电门时挡光.传送带水平部分的长度L=8m,沿逆时针方向以恒定速度v=6m/s匀速转动.物块A、B与传送带间的动摩擦因数μ=0.2,质量mA=mB=1kg.开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,并迅速移去轻弹簧,两物块第一次通过光电门,计时器显示读数均为t=9.0×10-4 s,重力加速度g取10m/s2.
如图所示为光电计时器的实验简易示意图.当有不透光物体从光电门间通过时,光电计时器就可以显示物体的挡光时间.光滑水平导轨MN上放置两个相同的物块A和B,左端挡板处有一弹射装置P,右端N处与水平传送带平滑连接,今将挡光效果好,宽度为d=3.6×10-3 m的两块黑色磁带分别贴在物块A和B上,且高出物块,并使高出物块部分在通过光电门时挡光.传送带水平部分的长度L=8m,沿逆时针方向以恒定速度v=6m/s匀速转动.物块A、B与传送带间的动摩擦因数μ=0.2,质量mA=mB=1kg.开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,并迅速移去轻弹簧,两物块第一次通过光电门,计时器显示读数均为t=9.0×10-4 s,重力加速度g取10m/s2.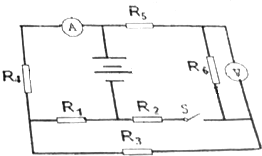 如图所示的电路中,电源的电动势E=13.5V,内阻r=2Ω,R4=2Ω,R5=1Ω,R6=3Ω电流表,电压表均为理想表,当开关闭合时电流表示数为1.5A,电压表示数为2.25V,当开关断开时电流表示数为1.35A,电压表示数为1.35V,问R1,R2,R3阻值分别为多少?
如图所示的电路中,电源的电动势E=13.5V,内阻r=2Ω,R4=2Ω,R5=1Ω,R6=3Ω电流表,电压表均为理想表,当开关闭合时电流表示数为1.5A,电压表示数为2.25V,当开关断开时电流表示数为1.35A,电压表示数为1.35V,问R1,R2,R3阻值分别为多少?