题目内容
15. 如图所示,在x轴上方有垂直纸面向里的匀强磁场,磁感应强度大小为B,在原点O处有一粒子源,t=0时刻沿纸面内的各个方向同时发射一群速率相同、质量为m、电荷量为+q的粒子,其中一个与x轴正方向成60°角射入磁场的粒子在t1时刻到达A点(图中未画出),A点为该粒子运动过程中距离x轴的最远点,且OA=L.不计粒子间的相互作用和粒子的重力,下列结论正确的是( )
如图所示,在x轴上方有垂直纸面向里的匀强磁场,磁感应强度大小为B,在原点O处有一粒子源,t=0时刻沿纸面内的各个方向同时发射一群速率相同、质量为m、电荷量为+q的粒子,其中一个与x轴正方向成60°角射入磁场的粒子在t1时刻到达A点(图中未画出),A点为该粒子运动过程中距离x轴的最远点,且OA=L.不计粒子间的相互作用和粒子的重力,下列结论正确的是( )| A. | 粒子的速率为qBL2m | |
| B. | 粒子的速率为√3qBL3m | |
| C. | t1时刻仍在磁场中的所有粒子均处在以O点为圆心、L为半径的14圆周上 | |
| D. | t1时刻仍在磁场中的所有粒子均处在以O点为圆心、L为半径的13圆周上 |
分析 粒子仅受洛伦兹力,做匀速圆周运动,根据已知画出离子的运动轨迹,然后求解即可.
解答 解:AB、如图,因OA=L,依据几何关系,则有粒子的半径R=√33L,
根据洛伦兹力提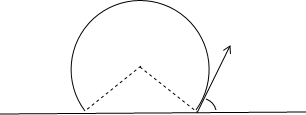 供向心力得qvB=mv2R,解得v=√3qBL3m,故A错误,B正确;
供向心力得qvB=mv2R,解得v=√3qBL3m,故A错误,B正确;
CD、如图可知,离子轨迹圆心角为120度,故C错误,D正确;
故选:BD.
点评 此题考查根据左手定则找出离子的运动轨迹,应用公式qvB=mv2R,并根据数学知识判断选项.

练习册系列答案
相关题目
6.如果把太阳系各行星的运动近似看作匀速圆周运动,则离太阳越近的行星( )
| A. | 周期越小 | B. | 环绕速度越小 | C. | 角速度越小 | D. | 加速度越小 |
3.某同学在用油膜法估测分子直径的实验中,计算结果明显偏大,可能是由于 ( )
| A. | 油酸未完全散开 | |
| B. | 油酸中含有大量的酒精 | |
| C. | 计算油膜面积时舍去了所有不足一格的方格 | |
| D. | 求每滴体积时,1mL的溶液的滴数少记了10滴 |
20.有一种硬气功表演:表演者平卧地面,将一大石板置于他的身体上,另一人将重锤举到高处并砸向石板,石板被砸碎,而表演者却安然无恙.我们发现,表演者在表演时都尽量挑选质量较大的石板.假设重锤与石板撞击后二者具有相同的速度,那么对这一现象,下列说法中正确的是( )
| A. | 重锤在与石板撞击的过程中,重锤与石板的总机械能守恒 | |
| B. | 石板的质量越大,石板获得的动量就越小 | |
| C. | 石板的质量越大,石板所受到的打击力就越小 | |
| D. | 石板的质量越大,石板获得的速度就越小 |
7. 如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
 如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )| A. | 物块a的重力势能减少mgh | |
| B. | 摩擦力对a做的功等于a机械能的增量 | |
| C. | 摩擦力对a做的功等于物块a、b动能增量之和 | |
| D. | 任意时刻,重力对a、b做功的瞬时功率大小相等 |
5.已知下面的哪组数据,可以算出地球的质量(引力常量G已知)( )
| A. | 月球绕地球运动的周期T1及月球到地球中心的距离R1 | |
| B. | 地球绕太阳运行周期T2及地球到太阳中心的距离R2 | |
| C. | 人造卫星的质量和它在地面附近的运行速度v3 | |
| D. | 地球绕太阳运行的速度v4及地球到太阳中心的距离R4 |


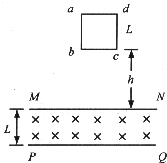 如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求:
如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求: