��Ŀ����
2��Ϊ����̽�������Ϻ����������ˡ���������ͼ����ʾ��ij̽����ѧϰС��ԡ����������ܽ����о��������á�������ˮƽ�������ɾ�ֹ��ʼ�˶��������������˶���ȫ���̼�¼������ͨ�����ݴ����õ���ͼ����ʾ��v-tͼ����֪0��t1��Ϊ��ԭ�����бֱ�ߣ�t1��10s�ڡ�����ǣ�����Ĺ��ʱ��ֲ��䣬��P=1.2kW��7��10s��Ϊƽ��F�����ֱ�ߣ���10sδֹͣң�أ��á��������ɻ��У�����������m=100kg�����������С������ܵ�������f��С���䣮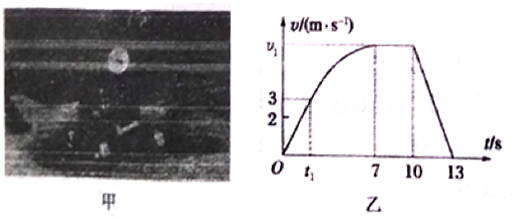
��1����������������f�Ĵ�С�͡����������˶�ʱ���ٶȴ�С��
��2���������ڼ����˶������е���λ��s��
��3����0��13s��ǣ�����������ܹ���
���� ��1����10sĩ��ȥǣ������С��ֻ���������������ȼ����˶��������ٶ�ͼ���б��������ٶȣ���ţ�ٵڶ����������������ٶȣ�
��2��Ӧ��ţ�ٵڶ��������˶�ѧ��ʽ��������˶����̵���λ�ƣ�
��3���������ǣ�����Ĺ���Ȼ������ܹ���
��� �⣺��1����10 sĩ��ȥǣ����������ֻ������f���������ȼ����˶���
��ͼ���֪�����ٶȣ�a=$\frac{��v}{��t}$=$\frac{{v}_{1}}{3}$��
��ţ�ٵڶ����ɵã���������f=ma��
7��10 s�ڡ����������˶�����ǣ����ΪF����F=f
��P=Fv1�ɵá����������˶�ʱ���ٶȣ�v1=$\frac{P}{F}$=$\frac{P}{f}$��
���v1=6 m/s��a=2m/s2��f=200N��
��2���������ļ��ٶ��˶����̿ɷ�Ϊ��
0��t1ʱ���ڵ��ȼ����˶���t1��7 sʱ���ڵı�����˶������Σ�
t1ʱ����ΪP=1.2kW���ٶ�Ϊ��vt=3 m/s��
��P=F1vt�ɵã���ʱǣ����ΪF1=$\frac{P}{{v}_{t}}$=400N��
��ţ�ٵڶ����ɣ�F1-f=ma1��
���0��t1ʱ���ڵļ��ٶȴ�СΪ��
a1=$\frac{{F}_{1}-f}{m}$=2m/s2��
�ȼ����˶���ʱ�䣺t1=$\frac{{v}_{t}}{{a}_{1}}$=1.5 s��
�ȼ����˶���λ�ƣ�s1=$\frac{1}{2}$a1t12=2.25m��
0-7s�ڣ��ɶ��ܶ����ã�F1s1+P��7-t1��-fs=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02��
��á������ڼ����˶������е���λ��s=28.5m��
��3����0��1.5 s�ڣ�ǣ����������W1=F1s1=400��2.25J=900J��
��1.5��10 s�ڣ�ǣ����������W2=P��t=1 200����10-1.5��J=10200J��
10s��ֹͣң�أ�ǣ��������Ϊ�㣬
0��13s��ǣ�����������ܹ���W=W1+W2=11100J��
�𣺣�1����������������f�Ĵ�СΪ200N�������������˶�ʱ���ٶȴ�СΪ2m/s2��
��2���������ڼ����˶������е���λ��sΪ28.5m��
��3����0��13s��ǣ�����������ܹ�Ϊ11100J��
���� �������ȿ��������ٶ�ͼ�����������ο������ͼ�����Ϣ�о������˶������Ӧ�ö��ܶ����������˶��б���������������

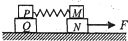 ��ͼ��ʾ���⻬ˮƽ���Ϸ��ô�M��N��P��Q�ĸ�ľ�飬����P��M������Ϊm��N��Q������Ϊ2m����P֮����һ���ʵ�������������ˮƽ����F��N��ʹ�ĸ�ľ����ͬһ���ٶ�a�����˶�������ͻȻ��ȥF˲�䣬����˵����ȷ���ǣ�������
��ͼ��ʾ���⻬ˮƽ���Ϸ��ô�M��N��P��Q�ĸ�ľ�飬����P��M������Ϊm��N��Q������Ϊ2m����P֮����һ���ʵ�������������ˮƽ����F��N��ʹ�ĸ�ľ����ͬһ���ٶ�a�����˶�������ͻȻ��ȥF˲�䣬����˵����ȷ���ǣ�������| A�� | PQ���Ħ�������� | B�� | M��P�ļ��ٶȴ�С��Ϊ$\frac{1}{2}$a | ||
| C�� | MN���Ħ�������� | D�� | N�ļ��ٶȴ�С��Ϊa |
 ��ͼ��ʾ��PQ��MN�Ƿ�����ˮƽ���ڵĹ⻬���죬GH�dz���ΪL������Ϊr�ĵ���������е���һ�˹̶����ᵯ�����ӣ��ᵯ�ɵľ���ϵ��Ϊk����������ڷ������¡��Ÿ�Ӧǿ��ΪB����ǿ�糡�У�ͼ��E�ǵ綯��ΪE�����費�Ƶ�ֱ����Դ���������ĵ���ΪC���պϿ��أ�����·�ȶ�������ѡ�������ǣ�������
��ͼ��ʾ��PQ��MN�Ƿ�����ˮƽ���ڵĹ⻬���죬GH�dz���ΪL������Ϊr�ĵ���������е���һ�˹̶����ᵯ�����ӣ��ᵯ�ɵľ���ϵ��Ϊk����������ڷ������¡��Ÿ�Ӧǿ��ΪB����ǿ�糡�У�ͼ��E�ǵ綯��ΪE�����費�Ƶ�ֱ����Դ���������ĵ���ΪC���պϿ��أ�����·�ȶ�������ѡ�������ǣ�������| A�� | ������е���Ϊ $\frac{E}{{R}_{2}+r{+R}_{1}}$ | B�� | �ᵯ�ɵij������� $\frac{BLE}{k��r{+R}_{1}��}$ | ||
| C�� | �ᵯ�ɵij��ȼ��� $\frac{BLE}{k��r{+R}_{1}��}$ | D�� | ������������Ϊ $\frac{E}{r{+R}_{1}}$CR |
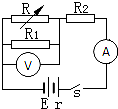 ��ͼ��ʾ�ĵ�·�У���Դ�綯��ΪE������Ϊr���������ɱ����R����ֵ����ʹ��ѹ����ʾ����С��U��������ʾ���仯��I���������Ϊ������������������У�������
��ͼ��ʾ�ĵ�·�У���Դ�綯��ΪE������Ϊr���������ɱ����R����ֵ����ʹ��ѹ����ʾ����С��U��������ʾ���仯��I���������Ϊ������������������У�������| A�� | R2���˵ĵ�ѹ���ӣ�������һ�����ڡ�U | |
| B�� | ���������ֵһ����С��������ʾ��һ������ | |
| C�� | ��U-��I•R2=��I•r | |
| D�� | $\frac{��U}{��I}=r+{R_2}$ |
| A�� | ÿ�����ɵĴ�����������ԭ����4������ɼ�ľ���Ҳ��Ϊԭ����4�� | |
| B�� | ���ֵ��ɵĴ��������䣬ʹ������ɼ�ľ�������ԭ����2�� | |
| C�� | ʹһ�����ɵĵ�����ӱ�����һ�����ɵĵ�������ֲ��䣬ͬʱ���������ɼ�ľ����СΪԭ����$\frac{1}{2}$ | |
| D�� | ���ֵ��ɵĵ�������䣬���������ɵľ����С��ԭ����$\frac{1}{2}$ |
 ��ͼ��ʾ���������õı��������ڹ⻬��ˮƽ���ϣ����̶������ú�����ΪS=1.0��10-2m2�Ĺ⻬��������һ�������������������������ڣ������˵���һ�˹̶���ǽ�ϣ��������¶�Ϊ27��ʱ����������ǽ�պ���ѹ���Ҵ�ʱ�ܱ���������Ϊ2.0��10-3m3����֪������ѹǿp0=1.0��105Pa��
��ͼ��ʾ���������õı��������ڹ⻬��ˮƽ���ϣ����̶������ú�����ΪS=1.0��10-2m2�Ĺ⻬��������һ�������������������������ڣ������˵���һ�˹̶���ǽ�ϣ��������¶�Ϊ27��ʱ����������ǽ�պ���ѹ���Ҵ�ʱ�ܱ���������Ϊ2.0��10-3m3����֪������ѹǿp0=1.0��105Pa��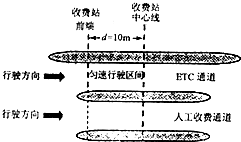 2015��9��28�գ����ɹš����������������½���ʡ��ʽ������ٹ�·���Ӳ�ͣ���շѣ�ETC������ϵͳ�����ˣ����ٹ�·ETCϵͳ����ʵ��ȫ�����������ء����ϳ��⣩������ʻ����ٹ�·ʱ���ֱ�ͨ��ETCͨ�����˹��շ�ͨ����������ͼ��ʾ���������������շ�վǰ��ʱ�ٶ�Ϊv1=5m/s�������ETCͨ����ֻ������ͨ�������ߺ����ȼ�����V2=15m/s��������ʻ��������˹��շ�ͨ������ǰ�˿�ʼ�ȼ����������ߴ��ٶ�ǡ��Ϊ0������T=20s�ɷѳɹ��������������ȼ�����v2������ʻ����֪�շ�վǰ�˺�������ľ���d=10m�����������ٹ����еļ��ٶȴ�СΪa=2m/s2���������ӽ����շ�վǰ�˵��ٴμ��ٵ�v2��
2015��9��28�գ����ɹš����������������½���ʡ��ʽ������ٹ�·���Ӳ�ͣ���շѣ�ETC������ϵͳ�����ˣ����ٹ�·ETCϵͳ����ʵ��ȫ�����������ء����ϳ��⣩������ʻ����ٹ�·ʱ���ֱ�ͨ��ETCͨ�����˹��շ�ͨ����������ͼ��ʾ���������������շ�վǰ��ʱ�ٶ�Ϊv1=5m/s�������ETCͨ����ֻ������ͨ�������ߺ����ȼ�����V2=15m/s��������ʻ��������˹��շ�ͨ������ǰ�˿�ʼ�ȼ����������ߴ��ٶ�ǡ��Ϊ0������T=20s�ɷѳɹ��������������ȼ�����v2������ʻ����֪�շ�վǰ�˺�������ľ���d=10m�����������ٹ����еļ��ٶȴ�СΪa=2m/s2���������ӽ����շ�վǰ�˵��ٴμ��ٵ�v2��