Question

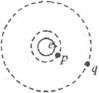
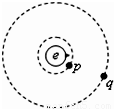
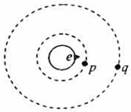
如图，地球赤道上山丘e，近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动．设e、p、q做匀速圆周运动的速率分别为υ_e、υ_p、υ_q，向心加速度分别为a_e、a_p、a_q，则（　　）

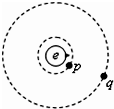
A．ae＜aq＜ap

B．ae＞ap＞aq

C．υe＜υp＜υq

D．υp＞υq＞υe

Answer 1

1、对于A、B选项：
对于p和q来说有G

Mm

R2

=ma
可得a=

GM

R

由于R_p＜R_q
则a_p＞a_q
根据a=ω²R
由于R_q＞R_e
可得a_q＞a_e
故a_p＞a_q＞a_e
故A正确，B错误．
2、对于C、D选项：
对于卫星来说根据万有引力提供向心力有
G

Mm

R2

=m

v2

R

解得v=

GM R

；
故卫星的轨道半R径越大，卫星的线速度v越小．
由于近地资源卫星p的轨道半径小于同步通信卫星q的轨道半径，
故同步卫星q的线速度v_q小于近地资源卫星p的线速度v_p，
即v_q＜v_p．
由于同步通信卫星q和赤道上的山丘e的角速度相同，到地心的距离R_q＞R_e
即ω_e=ω_q
根据v=ωR可得
v_e=ω_eR_e
v_q=ω_qR_q
即v_q＞v_e
故υ_p＞υ_q＞υ_e
故C错，D正确．
故选AD．