题目内容

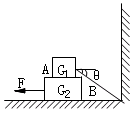
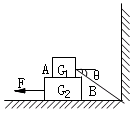
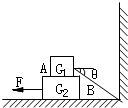在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如图所示，已知sinθ= $数学公式$ ，cosθ= $数学公式$ ，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？

解：物体A、B的受力图如图所示，由受力平衡知：

对A：Tcosθ-f₁=0…①
N₁-G₁-Tsinθ=0…②
又由题 $\text{[math]}$ ③
联立得到：Tcosθ=μ（G₁+Tsinθ）
得到T= $\text{[math]}$
f₁=Tcosθ
N₁=G₁+Tsinθ
对B： $\text{[math]}$ …④
$\text{[math]}$ …⑤
又f₂=μN₂…⑥
联立得到F=f₁+μ（N₁+G₂）
代入解得：F=850N
答：要把木板从货箱下抽出来，F至少应为850N．
分析：当把木板恰好从货箱下抽出来时，货箱与木板间、木板与地面间的静摩擦力达到最大值，根据平衡条件和摩擦力公式，分别研究A、B求解F的最小值．
点评：本题是两个物体的平衡问题，采用隔离法研究的，也可以先用整体法作出力图（如上面右图），再隔离A或B研究．

练习册系列答案

期末测试卷系列答案

小学培优总复习系列答案

小学科学探究手册系列答案

小学达标训练系列答案

小学毕业综合复习系列答案

小学毕业特训卷系列答案

小学毕业升学总复习系列答案

小学毕业升学模拟试卷系列答案

打好双基名校名师模拟卷系列答案

归类复习模拟试卷系列答案

相关题目

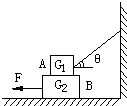在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如图所示，已知tgθ=3/4，然后在木板上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？

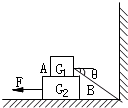（2011?东莞二模）在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如图所示，已知sinθ=

，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？

在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如图所示，已知sinθ=3/5,cosθ=4/5，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？

（10分）在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如图所示，已知sinθ=3/5,cosθ=4/5，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？

在水平地面上放一木板B，重力为G₂=100N，再在木板上放一货箱A，重力为G₁=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如下图所示，已知sinθ=0.6，cosθ=0.8，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？