题目内容
【题目】如图所示，半径R=1m的光滑半圆轨道AC与高h=8R的粗糙斜面轨道BD放在同一竖直平面内，BD部分水平长度为x=6R。两轨道之间由一条光滑水平轨道相连，水平轨道与斜轨道间有一段圆弧过渡。在水平轨道上，轻质弹簧被a、b两小球挤压（不连接），处于静止状态。同时释放两个小球，a球恰好能通过半圆轨道最高点A，b球恰好能到达斜面轨道最高点B。已知a球质量为m1=2kg，b球质量为m2=1kg，重力力加速度为g=10m/s2。（sin37°=0.6，cos37°=0.8）求：
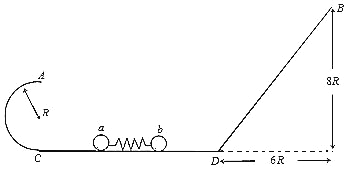
(1)a球经过C点时对轨道的作用力；
(2)释放小球前弹簧的弹性势能Ep；
(3)小球与斜面间动摩擦因素μ.
【答案】(1)FC=120N,方向竖直向下 (2)EP=150J (3) 
【解析】（1）由a球恰好能到达A点，重力提供向心力，有： 
a球从C到A的过程，由机械能守恒定律得： 
m1vC2-
m1vA2=m1g2R
得，小球a经过C点的速度： 
在C点，以a球为研究对象，由牛顿第二定律得： 
联立解得：N=6m1g=120N
由牛顿第三定律知，a球经过C点时对轨道的作用力大小为120N，方向竖直向下．
（2）对ab系统，在弹簧释放的瞬时动量守恒，则：m1va-m2vb=0
解得：vb=10
m/s
（3）由数学知识可知斜面的倾角为53°，长度为10R．
对于b球沿斜面上滑的过程，由动能定理得：0-
m2vb2=-m2g8R-μm2gcos53°10R
解得: 
练习册系列答案
相关题目
